题目内容

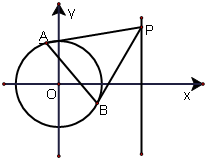
圆C：（x-1）2+（y-2）2=25内有一点P（3，1），l为过点P且倾斜角为α的直线．
（1）若α=
3π
4
，求直线l与圆C相交弦的弦长；
（2）求直线l被圆C截得的弦长度最短时，直线l的方程．
（1）α=
3π
4
⇒kl=-1，
直线l的方程：y-1=-（x-3）即x+y-4=0
点C（1，2）到直线l的距离d=
|1+2-4|
2
=
2
2
，又圆C的半径为5，
则直线l与圆C相交弦的弦长为：2
52-(
2
2
)2
=7
2
；
（2）当直线l与直线CP垂直时，直线l被圆C截得的弦长度最短.kCP=-
1
2
⇒kl=2
∴直线l的方程：2x-y-5=0．
练习册系列答案
相关题目
由圆x2+y2=1外一点P（2，1）引圆的切线，切线长为（　　）
A．
5
B．2C．1D．4
已知圆x2+y2=8内一点P0（-1，2），AB为过点P0且倾斜角为α的弦．
（1）当α=135°时，求AB的长．
（2）当弦AB最长时，求出直线AB的方程．
（3）当弦AB被点P0平分时，求出直线AB的方程．
在平面直角坐标系xOy中，已知圆C的方程为x2+y2-8x+15=0，直线l的方程为y=kx-2．
（1）若直线l被圆C所截得弦长为2，求直线l的方程；
（2）若直线l上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，求k的最大值．
已知圆C的圆心为原点O，且与直线x+y+4
2
=0相切．
（1）求圆C的方程；
（2）点P在直线x=8上，过P点引圆C的两条切线PA，PB，切点为A，B，求证：直线AB恒过定点．
设P（x，y）是曲线C：
x=-2+cosθ
y=sinθ
(θ为参数，0≤θ＜2π）上任意一点，则
y
x
的取值范围是（　　）
A．[-
3
，
3
]		B．(-∞，-
3
]∪[
3
，+∞)
C．[-
3
3
，
3
3
]		D．(-∞，-
3
3
]∪[
3
3
，+∞)
若实数x、y满足等式（x-2）2+y2=3，那么x+2y的最大值为______．
直线y=-x-b与曲线x=
1-y2
有且只有一个交点，则b的取值范围是______．
若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心，则a的值为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网