题目内容
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数f(x)=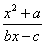 (b,c∈N)有且只有两个不动点0,2,且f(-2)<
(b,c∈N)有且只有两个不动点0,2,且f(-2)<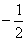 ,
,
(1)求函数f(x)的解析式;
(2)已知各项不为零的数列{an}满足4Sn·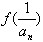 =1(Sn为数列前n项和),求数列{an}的通项公式an;
=1(Sn为数列前n项和),求数列{an}的通项公式an;
(3)如果数列{an}满足a1=4,an+1=f(an),求证:当n≥2时,恒有an<3成立.
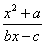 (b,c∈N)有且只有两个不动点0,2,且f(-2)<
(b,c∈N)有且只有两个不动点0,2,且f(-2)<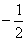 ,
,(1)求函数f(x)的解析式;
(2)已知各项不为零的数列{an}满足4Sn·
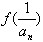 =1(Sn为数列前n项和),求数列{an}的通项公式an;
=1(Sn为数列前n项和),求数列{an}的通项公式an;(3)如果数列{an}满足a1=4,an+1=f(an),求证:当n≥2时,恒有an<3成立.
解:(1)依题意有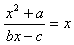 ,化简得(1-b)x2+cx+a=0,
,化简得(1-b)x2+cx+a=0,
由韦达定理,得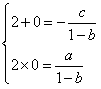 ,解得
,解得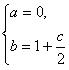 ,
,
代入表达式得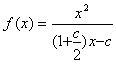 ,
,
由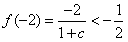 得c<3,
得c<3,
又c∈N,b∈N,
若c=0,b=1,则f(x)=x,不满足题意,
∴c=2,b=2,
故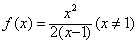 。
。
(2)由题设得 ,得:
,得: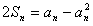 , (*)
, (*)
且an≠1,用n-1代n得: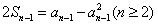 ,(**)
,(**)
(*)与(**)两式相减得: ,
,
即 ,
,
∴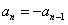 或
或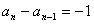 ,
,
把n=1代入(*)得: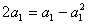 ,
,
解得a1=0(舍去)或a1=-1,
若 ,得a2=1,这与an≠1矛盾,
,得a2=1,这与an≠1矛盾,
∴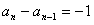 ,即{an}是以-1为首项,-1为公差的等差数列,
,即{an}是以-1为首项,-1为公差的等差数列,
∴an=-n。
(3)采用反证法,假设an≥3(n≥2),则由(1)知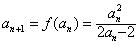 ,
,
∴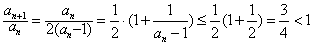 ,
,
即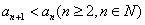 ,有
,有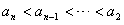 ,
,
而当n=2时,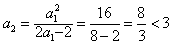 ,
,
∴an<3,这与假设矛盾,故假设不成立,
∴an<3。

练习册系列答案
相关题目
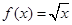 的等域区间是 .
的等域区间是 .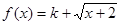 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.