题目内容
(本小题满分6分）对于函数f(x)，若存在x0ÎR，使f(x0)＝x0成立，则称点(x0，x0)为函数的不动点，已知函数f(x)＝ax2＋bx-b有不动点(1,1)和(-3,-3)，求a、b的值。
【解析】略
(本小题满分12分)
某班甲、乙两名同学参加l00米达标训练，在相同条件下两人l0次训练的成绩(单位：秒)如下：
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
甲 |
11.6 |
12.2 |
13.2 |
13.9 |
14.0 |
11.5 |
13.1 |
14.5 |
11.7 |
14.3 |
|
乙 |
12.3 |
13.3 |
14.3 |
11.7 |
12.0 |
12.8 |
13.2 |
13.8 |
14.1 |
12.5 |
(I)请作出样本数据的茎叶图；如果从甲、乙两名同学中选一名参加学校的100米比赛，从成绩的稳定性方面考虑，选派谁参加比赛更好，并说明理由(不用计算，可通过统计图直接回答结论)．
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次，求抽取的成绩中至少有一个比12．8秒差的概率．
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计，甲、乙的成绩都均匀分布在[11．5，14．5]
之间，现甲、乙比赛一次，求甲、乙成绩之差的绝对值小于0．8秒的概率．
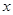（单位：cm）满足关系：
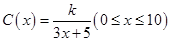，若不建隔热层，每年能源消耗费用为8万元．设
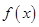为隔热层建造费用与20年的能源消耗费用之和．
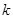的值及
（本小题满分6分）某高级中学共有学生3000名,各年级男、女生人数如下表：
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 487 |
|
|
| 男生 | 513 | 560 |
|
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是
.
问高二年级有多少名女生?
现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生?
（本小题满分6分）某高级中学共有学生3000名,各年级男、女生人数如下表：
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 487 |
|
|
| 男生 | 513 | 560 |
|
已知在全校学生中随机抽取1名，抽到高二年级女生的概率是
.
问高二年级有多少名女生?
现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生?