题目内容
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数
f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证:![]() <m<1;
<m<1;
⑵若|x1|<2且|x1-x2|=2,求b的取值范围.
见解析
解析:
(Ⅰ)证明:g(x)=f(x)-x=ax2+(b-1)x+1?且a>0 ∵x1<1<x2<2
∴(x1-1)(x2-1)<0即x1x2<(x1+x2)-1
于是![]()
>![]() [(x1+x2)-1]=
[(x1+x2)-1]=![]()
又∵x1<1<x2<2 ∴x1x2>x1于是有m=![]() (x1+x2)-
(x1+x2)-![]() x1x2<
x1x2<![]() (x1+x2)-
(x1+x2)-![]() x1=
x1=![]() x2<1 ∴
x2<1 ∴![]() <m<1
<m<1
(Ⅱ)解:由方程![]() >0,∴x1x2同号
>0,∴x1x2同号
(ⅰ)若0<x1<2则x2-x1=2
∴x2=x1+2>2 ∴g(2)<0
即4a+2b-1<0 ①
又(x2-x1)2=![]()
∴![]() ,(∵a>0)代入①式得
,(∵a>0)代入①式得
![]() <3-2b,解之得:b<
<3-2b,解之得:b<![]()
(ⅱ)若-2<x1<0,则x2=-2+x1<-2 ∴g(-2)<0,即4a-2b+3<0 ②
又![]() 代入②得
代入②得![]() <2b-1解之得b>
<2b-1解之得b>![]()
综上可知b的取值范围为![]()

练习册系列答案
相关题目
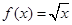 的等域区间是 .
的等域区间是 .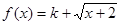 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.