Question

对于函数f(x)，若在其定义域内存在两个实数a，b(a＜b)，使当x∈[a，b]时，f(x)的值域也是[a，b]，则称函数f(x)为“布林函数”，区间[a，b]称为函数f(x)的“等域区间”.

（1）布林函数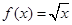的等域区间是         .

（2）若函数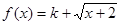是布林函数，则实数k的取值范围是           .

 

Answer 1

【答案】

（1）[0,1]；（2）.

【解析】

试题分析：（1）因为是增函数，则当x∈[a，b]时，f(x)∈[f(a)，f(b)].

令f(a)＝a，且f(b)＝b，即，且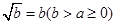，则a＝0，b＝1.

故布林函数的等域区间是[0,1].

（2）

因为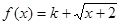是增函数，若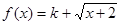是布林函数，则

存在实数a，b(－2≤a＜b)，使，即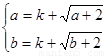.所以a，b为方程的两个实数根，从而方程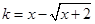有两个不等实根.

令，则.当时，；当时，.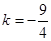

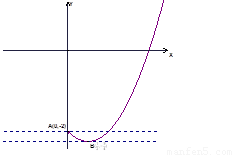
由图可知，当时，直线与曲线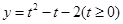有两个不同交点，即方程

有两个不等实根，故实数k的取值范围是.

考点：新概念的理解、方程的根与函数的图像