题目内容
函数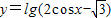 的单调递增区间为( )
的单调递增区间为( )A.(2kπ+π,2kπ+2π)(k∈Z)
B.
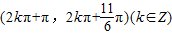
C.
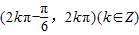
D.
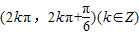
【答案】分析:根据对数函数的真数必须为正,结合余弦函数的图象和性质,先求出函数的定义域,进而分析内外函数的单调性,结合复合函数“同增异减”的原则可得函数的单调递增区间.
解答:解:要使函数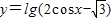 的解析式有意义
的解析式有意义
自变量x须满足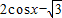 >0,即
>0,即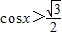
解得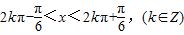
∵函数y=lgu为增函数,u=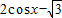 在
在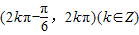 上为增函数
上为增函数
∴ 为函数
为函数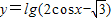 的单调递增区间
的单调递增区间
故选C
点评:本题考查的知识点是复合函数的单调性,其中本题易忽略函数的定义域,而错选A.
解答:解:要使函数
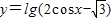 的解析式有意义
的解析式有意义自变量x须满足
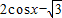 >0,即
>0,即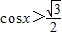
解得
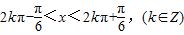
∵函数y=lgu为增函数,u=
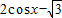 在
在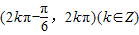 上为增函数
上为增函数∴
 为函数
为函数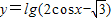 的单调递增区间
的单调递增区间故选C
点评:本题考查的知识点是复合函数的单调性,其中本题易忽略函数的定义域,而错选A.

练习册系列答案
相关题目
 的单调递增区间为________________
的单调递增区间为________________ 的单调递增区间为
。
的单调递增区间为
。