题目内容
8.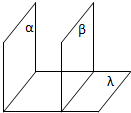 如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.
如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.
分析 要证平面β⊥平面γ,可证平面β经过了平面γ的一条垂线,由平面α⊥平面γ,可在平面α找到一条与平面γ垂直的直线,再由平面α∥平面β,利用两平面平行的性质在平面β内找到一条与平面γ垂直的直线,则问题得证.
解答  证明:如图,
证明:如图,
∵平面α⊥平面γ,∴平面α与平面γ相交,设交线为m,
在平面α内作直线a⊥m,∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O,由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β,由面面平行的判定定理,得a∥b,
∵a∥b,a⊥γ,∴b⊥γ
又∵b?β,
∴平面β⊥平面γ.
点评 本题考查了平面与平面垂直的判定,考查了平面与平面垂直的性质,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
20.方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=-1}\end{array}\right.$的解的集合是( )
| A. | {x=1,y=2} | B. | {1,2} | C. | {(x,y)|x=1或y=2} | D. | {(1,2)} |
17.已知函数y=4x+$\frac{1}{x}$(x>0),那么当y取得最小值时,x的值是( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |