题目内容
11.函数y=3x2+ax+4在区间[-1,1]上不是单调函数,则实数a的取值范围是( )| A. | (-6,6) | B. | [-6,6] | C. | (-∞,-6]∪[6,+∞) | D. | (-∞,-6)∪(6,+∞) |
分析 由条件并结合二次函数y=3x2+ax+4的对称轴为x=-$\frac{a}{6}$,可得-1<-$\frac{a}{6}$<1,由此求得实数a的取值范围.
解答 解:二次函数y=3x2+ax+4的对称轴为x=-$\frac{a}{6}$,
∵y=3x2+ax+4在区间[-1,1]上不是单调函数,
∴-1<-$\frac{a}{6}$<1,解得-6<a<6,
故选:A.
点评 本题主要考查二次函数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)的定义域是[0,2],则函数g(x)=f(x+$\frac{1}{2}$)+f(x-$\frac{1}{2}$)的定义域是( )
| A. | [0,2] | B. | [$-\frac{1}{2}$,$\frac{3}{2}$] | C. | [$\frac{1}{2}$,$\frac{5}{2}$] | D. | [$\frac{1}{2}$,$\frac{3}{2}$] |
6.在1和100间插入n个正数,使这n+2个正数成等比数列,则插入的n个正数之积为 ( )
| A. | 10n | B. | n10 | C. | 100n | D. | n100 |
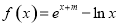 .
. 是函数
是函数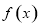 的极值点,求
的极值点,求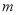 并讨论
并讨论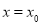 是函数
是函数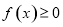 恒成立,求
恒成立,求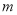 的取值范围(其中常数
的取值范围(其中常数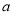 满足
满足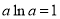 ).
).