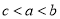题目内容
5.已知函数f(x)是定义在[-1,1]上的减函数.若f(1-x)-f(3x-1)≤0.求x的取值范围.分析 根据函数单调性的性质进行求解即可.
解答 解:∵f(1-x)-f(3x-1)≤0,
∴f(1-x)≤f(3x-1),
∵f(x)是定义在[-1,1]上的减函数,
∴$\left\{\begin{array}{l}{-1≤1-x≤1}\\{-1≤3x-1≤1}\\{1-x≥3x-1}\end{array}\right.$,即$\left\{\begin{array}{l}{0≤x≤2}\\{0≤x≤\frac{2}{3}}\\{x≤\frac{1}{2}}\end{array}\right.$,
解得0≤x≤$\frac{1}{2}$,
即x的取值范围是[0,$\frac{1}{2}$].
点评 本题主要考查不等式的求解,根据函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
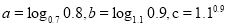 ,则
,则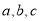 的大小关系是( )
的大小关系是( )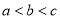 B.
B.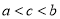
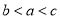 D.
D.