题目内容
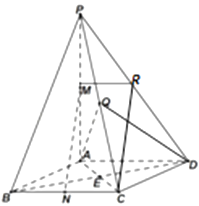
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点. 
(1)证明:直线MN∥平面PCD;
(2)若点Q为PC中点,∠BAD=120°,PA= ![]() ,AB=1,求三棱锥A﹣QCD的体积.
,AB=1,求三棱锥A﹣QCD的体积.
【答案】
(1)解:取PD中点R,连结MR,CR,
∵M是PA的中点,R是PD的中点,
∴MR= ![]() AD,MR∥AD,
AD,MR∥AD,
∵四边形ABCD是菱形,N为BC的中点,
∴NC= ![]() ,NC∥AD.
,NC∥AD.
∴NC∥MR,NC=MR,
∴四边形MNCR为平行四边形,
∴MN∥CR,又CR平面PCD,MN平面PCD,
∴MN∥平面PCD.
(2)解:∵四边形ABCD是菱形,∠BAD=120°,
∴AC=AD=CD=1,∴ ![]() .
.
∵Q是PC的中点,∴Q到平面ABCD的距离h= ![]() PA=
PA= ![]() .
.
∴ ![]() .
.
【解析】(1)取PD中点R,连结MR,CR,通过证明四边形MNCR是平行四边形得出MN∥CR,于是MN∥平面PCD;(2)棱锥Q﹣ACD的底面△ACD为等边三角形,高为PA的 ![]() ,代入体积公式计算即可.
,代入体积公式计算即可.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

