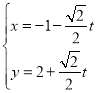题目内容
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() 是函数
是函数![]() 的导数.
的导数.
(1)若![]() 是
是![]() 上的单调函数,求
上的单调函数,求![]() 的值;
的值;
(2)当![]() 时,求证:若
时,求证:若![]() ,且
,且![]() ,则
,则![]() .
.
【答案】(1)![]() ,(2)证明见解析
,(2)证明见解析
【解析】
(1)对![]() 求导,可得
求导,可得![]() ,令
,令![]() 则
则![]() 恒成立,由于
恒成立,由于![]() ,所以
,所以![]() ,即可求出结果.
,即可求出结果.
(2)方法一:利用消元求导,由题意可得![]() ,
,
令![]() ,
,![]() ,不妨设
,不妨设![]() ,
,![]() ,
,
令![]()
![]() ,
,
原题即证明当![]() 时,
时,![]() ,利用导数在不等式中应用,即可求出结果.
,利用导数在不等式中应用,即可求出结果.
方法二:利用切线放缩法,化解过程同方法一,原题即证明当![]() 时,
时,![]() ,
,![]() ,注意到
,注意到![]() ,求出
,求出![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .下面证明
.下面证明![]() 恒成立(
恒成立(![]() );令
);令![]() ,然后再利用导数在不等式中应用,和不等式放缩即可证明结果.
,然后再利用导数在不等式中应用,和不等式放缩即可证明结果.
(1)![]() ,
,![]() ,由题意
,由题意![]() 恒成立,由于
恒成立,由于![]() ,所以
,所以![]() ,解得
,解得![]() .
.
方法一:消元求导死算
(2)![]()
![]() ,
,
令![]() ,
,![]() ,不妨设
,不妨设![]() ,
,![]() ,
,
令![]()
![]() ,
,
原题即证明当![]() 时,
时,![]() ,
,![]()
![]()
![]() ,其中
,其中
![]() ,因为
,因为![]() ,所以当
,所以当![]() 时,
时,![]() ,得证.
,得证.
方法二:切线放缩
化解过程同上,原题即证明当![]() 时,
时,![]() ,
,![]() ,注意到
,注意到![]() ,求出
,求出![]() 在
在![]() 处的切线方程,则
处的切线方程,则![]() ,即
,即![]() ,则:切线方程为
,则:切线方程为![]() .下面证明
.下面证明![]() 恒成立(
恒成立(![]() );令
);令![]() ,则
,则![]() ,得
,得![]() 在
在![]() 恒成立,故
恒成立,故![]() 在(
在(![]() )上单调递增,
)上单调递增,![]() 恒成立,故
恒成立,故![]() 恒成立,同理可证
恒成立,同理可证![]() 始终位于
始终位于![]() 在
在![]() 处的切线
处的切线![]() 的上方,即:
的上方,即:![]() (实际上
(实际上![]() 与
与![]() 关于
关于![]() 轴对称),故
轴对称),故![]()
![]() 恒成立,原不等式得证.
恒成立,原不等式得证.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案【题目】某企业拟对某条生产线进行技术升级,现有两种方案可供选择:方案![]() 是报废原有生产线,重建一条新的生产线;方案
是报废原有生产线,重建一条新的生产线;方案![]() 是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
是对原有生产线进行技术改造.由于受诸多不可控因素的影响,市场销售状态可能会发生变化.该企业管理者对历年产品销售市场行情及回报率进行了调研,编制出下表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期平均年利润(单位:万元) | 方案 | 700 | 400 |
|
方案 | 600 | 300 |
| |
(1)以预期平均年利润的期望值为决策依据,问:该企业应选择哪种方案?
(2)记该生产线升级后的产品(以下简称“新产品”)的年产量为![]() (万件),通过核算,实行方案
(万件),通过核算,实行方案![]() 时新产品的年度总成本
时新产品的年度总成本![]() (万元)为
(万元)为![]() ,实行方案
,实行方案时新产品的年度总成本
![]() (万元)为
(万元)为![]() .已知
.已知![]() ,
,![]() .若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价
.若按(1)的标准选择方案,则市场行情为畅销、平销和滞销时,新产品的单价![]() (元)分别为60,
(元)分别为60,![]() ,
,![]() ,且生产的新产品当年都能卖出去.试问:当
,且生产的新产品当年都能卖出去.试问:当![]() 取何值时,新产品年利润
取何值时,新产品年利润![]() 的期望取得最大值?并判断这一年利润能否达到预期目标.
的期望取得最大值?并判断这一年利润能否达到预期目标.
【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会,拟定地铁票价后又进行了一次调查.调查随机抽查了50人,他们的月收入情况与对地铁票价格态度如下表:
月收入(单位:百元) |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少(结果保留2位小数);
(2)由以上统计数据填写下面![]() 列联表分析是否有
列联表分析是否有![]() 的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附:![]()
| 0.05 | 0.01 |
| 3.841 | 6.635 |