题目内容
(本题满分13分)
射击比赛中,每位射手射击队10次,每次一发,击中目标得3分,未击中目标得0分,每射击一次,凡参赛者加2分,已知小李击中目标的概率为0.8.
(1)设X为小李击中目标的次数,求X的概率分布;
(2)求小李在比赛中的得分的数学期望与方差.
射击比赛中,每位射手射击队10次,每次一发,击中目标得3分,未击中目标得0分,每射击一次,凡参赛者加2分,已知小李击中目标的概率为0.8.
(1)设X为小李击中目标的次数,求X的概率分布;
(2)求小李在比赛中的得分的数学期望与方差.
(1)X的概率分布为
(2)设小李在比赛中的得分为Y,由(1)知满足二项分布 所以
所以
E(Y)=E(3X+2)=3E(X)+2=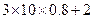 =26,
=26,
D(Y)=" D(3X+2)=9D(X)" = =14.4,
=14.4,
| X | O | 1 | … | 10 |
| P | 0.210 |  | … | 0.810 |
 所以
所以E(Y)=E(3X+2)=3E(X)+2=
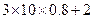 =26,
=26,D(Y)=" D(3X+2)=9D(X)" =
 =14.4,
=14.4,略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。
效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。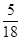


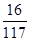
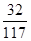
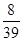
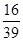
 有基本事件,并求出基本事件的个数;
有基本事件,并求出基本事件的个数;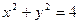 内的概率.
内的概率. 服从正态分布
服从正态分布 ,若
,若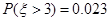 ,则
,则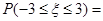 ( )
( ) 、
、
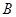 、
、
 、
、
 、
、
 两次摸出的球颜色相同的概率是 ;
两次摸出的球颜色相同的概率是 ;