题目内容
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线 相切,则a的取值范围是( )
相切,则a的取值范围是( )
A. | B. |
C.-3≤a≤一 或 或 ≤a≤7 ≤a≤7 | D.a≥7或a≤—3 |
C
解析试题分析:圆 ,圆心
,圆心 ,
, ,两直线分别与圆相切时对应的
,两直线分别与圆相切时对应的 的边界值:
的边界值: 时
时 ;
; 时,
时, 或
或 ,所以
,所以 的边界值分别为
的边界值分别为 ,所以选
,所以选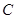 .
.
考点:1.点到圆的距离公式;2.直线与圆相切问题.

练习册系列答案
相关题目
若直线y=kx+4+2k与曲线 有两个交点,则k的取值范围是( ).
有两个交点,则k的取值范围是( ).
| A.[1,+∞) | B.[-1,-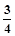 ) ) | C.(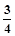 ,1] ,1] | D.(-∞,-1] |
直线 与圆
与圆 有两个不同交点,则
有两个不同交点,则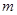 满足( ).
满足( ).
A. | B. | C. | D. |
直线 与圆C:
与圆C: 切于点
切于点 ,则a+b的值为( )
,则a+b的值为( )
| A.1 | B.-1 | C.3 | D.-3 |
已知直线 与曲线
与曲线 有交点,则( )
有交点,则( )
A. | B. | C. | D. |
已知实数 满足
满足 ,则
,则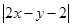 的最小值是( )
的最小值是( )
A. | B. | C. | D.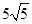 |
若直线 与圆
与圆 相切,则
相切,则 的值是 ( )
的值是 ( )
A.1, | B.2, | C.1 | D. |
 :
: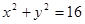 的周长和面积同时分为相等的两部分的函数称为圆
的周长和面积同时分为相等的两部分的函数称为圆



 的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则
的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则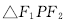 的面积为 ( )
的面积为 ( )