题目内容
向图3-3-13中所示正方形内随机地投掷飞标,
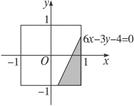
图3-3-13
求飞标落在阴影部分的概率.

图3-3-13
求飞标落在阴影部分的概率.
方法一:由于随机地投掷飞标,飞标落在正方形内每一个点的机会是等可能的,所以符合几何概型的条件.
S阴影=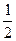 ×
×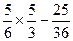 ,S正=22=4,
,S正=22=4,
∴P=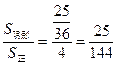 .
.
方法二:通过建立坐标系,得到两“长度”曲线的范围,才能对随机变量进行平移、伸缩变换,只有得到两“长度”曲线的方程,才能数出适合条件的数组数.
(1)利用计算器或计算机产生两组0至1区间内的均匀随机数a1、b1(共N组);
(2)经平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2;
(3)数出满足不等式b<2a-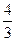 ,即6a-3b>4的数组数N1,
,即6a-3b>4的数组数N1,
所求概率P≈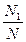 .可以发现,试验次数越多,概率P越接近
.可以发现,试验次数越多,概率P越接近 .
.
S阴影=
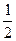 ×
×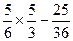 ,S正=22=4,
,S正=22=4,∴P=
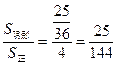 .
.方法二:通过建立坐标系,得到两“长度”曲线的范围,才能对随机变量进行平移、伸缩变换,只有得到两“长度”曲线的方程,才能数出适合条件的数组数.
(1)利用计算器或计算机产生两组0至1区间内的均匀随机数a1、b1(共N组);
(2)经平移和伸缩变换,a=(a1-0.5)*2,b=(b1-0.5)*2;
(3)数出满足不等式b<2a-
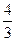 ,即6a-3b>4的数组数N1,
,即6a-3b>4的数组数N1,所求概率P≈
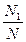 .可以发现,试验次数越多,概率P越接近
.可以发现,试验次数越多,概率P越接近 .
.几何概型问题一般有公式法和随机模拟两种方法,当然随机模拟方法比较麻烦,
在公式法不好进行的情况下可考虑随机模拟方法.
我们分别用两种方法计算该事件的概率:
(1)利用几何概型的公式;
(2)用随机模拟的方法.
在公式法不好进行的情况下可考虑随机模拟方法.
我们分别用两种方法计算该事件的概率:
(1)利用几何概型的公式;
(2)用随机模拟的方法.

练习册系列答案
相关题目
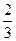 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为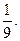
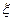 ,求
,求 ,
, ,
, 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于 分的共有多少人?
分的共有多少人?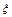 为成活沙柳的株数,数学期望E(
为成活沙柳的株数,数学期望E(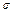 为
为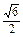 .
.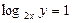 的概率为( ).
的概率为( ). 


