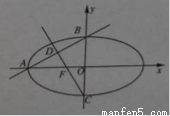
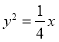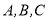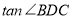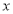题目内容
已知数列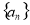 前n项和
前n项和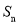 =
=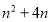 (
(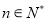 ), 数列
), 数列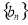 为等比数列,首项
为等比数列,首项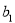 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足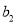 ,
,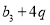 ,
,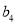 为等比数列.
为等比数列.
(1)求数列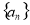 ,
,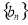 的通项公式;
的通项公式;
(2)设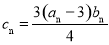 ,记数列
,记数列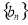 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
(1) ,
, ;(2)
;(2)
【解析】
试题分析:(1)因为数列 前n项和
前n项和 =
= (
( ),这类型一般都是通过向前递推一个等式,然后根据
),这类型一般都是通过向前递推一个等式,然后根据 .即可转化为关于通项的等式.但是要检验第一项是否成立. 数列
.即可转化为关于通项的等式.但是要检验第一项是否成立. 数列 为等比数列以及题所给的其他条件,即可求出通项公式.
为等比数列以及题所给的其他条件,即可求出通项公式.
(2)因为 ,又因为由(1)可得
,又因为由(1)可得 ,
, 的通项公式,即可求得数列
的通项公式,即可求得数列 的通项公式.再通过错位相减法求得前n项的和.
的通项公式.再通过错位相减法求得前n项的和.
试题解析:(1)当n=1时, .
.
当n≥2时,
 ,
,
验证 时也成立.∴数列
时也成立.∴数列 的通项公式为:
的通项公式为: ,
,
∵ 成等差数列,
成等差数列, 所以
所以 ,即
,即 ,
,
因为 ∴
∴ ∴数列
∴数列 的通项公式为:
的通项公式为: 6分
6分
(2)∵
∴ 
 ①
①
 ②
②
由①-②得:

∴ 12分
12分
考点:1.数列的通项与前n项和的关系式.2.等比数列.3.错位相减法.4.递推的数学思想.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目