题目内容
(本小题满分14分)已知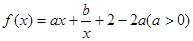 的图像在点
的图像在点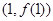 处的切线与直线
处的切线与直线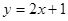 平行.
平行.
⑴ 求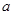 ,
,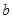 满足的关系式;
满足的关系式;
⑵ 若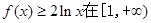 上恒成立,求
上恒成立,求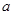 的取值范围;
的取值范围;
⑶ 证明: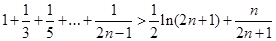 (
(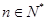 )
)
(1)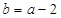 ;(2)
;(2)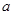 的取值范围是
的取值范围是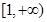 ;(3)见解析。
;(3)见解析。
解析试题分析:(Ⅰ)求导函数,利用图象在点(1,f(1))处的切线与直线y=2x+1平行,可得f′(1)=a-b=2,即可求a,b满足的关系式;
(Ⅱ)由(Ⅰ)知,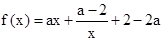 构造新函数g(x)=f(x)-2lnx=
构造新函数g(x)=f(x)-2lnx=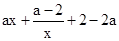 -2lnx,x∈[1,+∞)则根据g(1)=0,g′(x),比较对应方程根的大小,进行分类讨论,即可求得a的取值范围;
-2lnx,x∈[1,+∞)则根据g(1)=0,g′(x),比较对应方程根的大小,进行分类讨论,即可求得a的取值范围;
(1)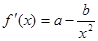 ,根据题意
,根据题意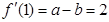 ,即
,即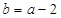 ………3分
………3分
(2)由(1)知,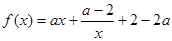 ,………4分
,………4分
令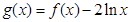
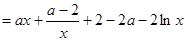 ,
,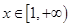
则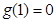 ,
,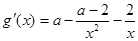 =
=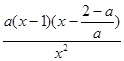 ………5分
………5分
①当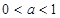 时,
时,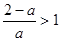 ,
,
若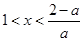 ,则
,则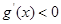 ,
,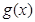 在
在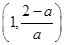 为减函数,存在
为减函数,存在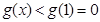 ,
,
即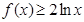 在
在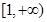 上不恒成立. ………6分
上不恒成立. ………6分
②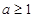 时,
时,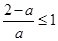 ,当
,当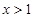 时,
时,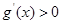 ,
,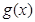 在
在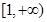 增函数,又
增函数,又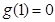 ,
,
∴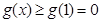 ,∴
,∴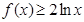 恒成立.………7分
恒成立.………7分
综上所述,所求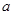 的取值范围是
的取值范围是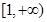 …………8分
…………8分
(3)由(2)知当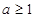 时,
时,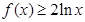 在
在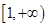 上恒成立.取
上恒成立.取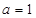 得
得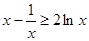
令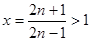 ,
,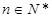 得
得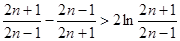 ,
,
即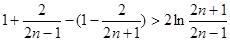 ……10分
……10分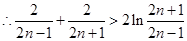
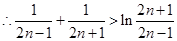
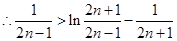
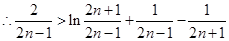
∴ ………11分
………11分
上式中令n=1,2,3,…,n,并注意到: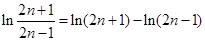
然后n个不等式相加得到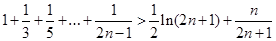 ………14分
………14分
考点:本试题主要考查了导数知识的运用,考查恒成立问题,考查不等式的证明。属于中档试题。
点评:解决该试题的关键是正确求出导函数,构造新函数,利用函数的单调性解题,这是解决一般不等式恒成立问题的常用的方法,也是比较重要的方法。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 为非负实数,函数
为非负实数,函数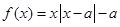 .
.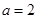 时,求函数的单调区间;
时,求函数的单调区间;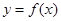 的零点个数.
的零点个数. 定义域为
定义域为 ,若对于任意的
,若对于任意的 ,都有
,都有 ,且
,且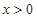 时,有
时,有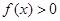 .
. ,若
,若 ,对所有
,对所有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的最小值;
的最小值;  的值域。
的值域。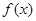 满足以下两个条件:
满足以下两个条件: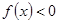 的解集是(-2,0) ②函数
的解集是(-2,0) ②函数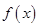 在
在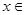
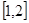 上的最小值是3
上的最小值是3 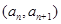
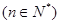 在函数
在函数
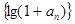 为等比数列
为等比数列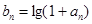 ,是否存在正实数
,是否存在正实数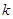 ,使不等式
,使不等式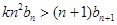 对于一切的
对于一切的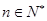 恒成立?若存在,指出
恒成立?若存在,指出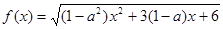 ,
, 的定义域为R,求实数
的定义域为R,求实数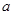 的取值范围.
的取值范围.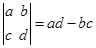
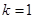 ,解关于
,解关于 的不等式
的不等式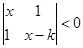
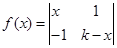 ,对任意
,对任意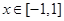 ,都有
,都有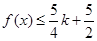 ,求实数
,求实数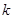 的取值范围。
的取值范围。 在(1,+∞)上是减函数.
在(1,+∞)上是减函数.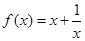 .
.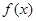 在
在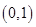 上是减函数;
上是减函数;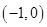 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).