题目内容
(本小题满分12分)
已知函数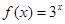 ,且
,且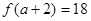 ,
,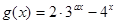 。
。
(1)求函数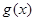 的解析式; (2)求函数
的解析式; (2)求函数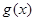 在
在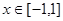 上的值域。
上的值域。
(1)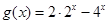 。
。
(2)函数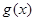 在
在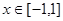 的上值域为
的上值域为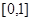 。
。
解析试题分析:(1)由已知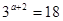 ,
,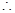
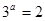 ,………………3分
,………………3分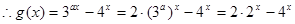 。………………6分
。………………6分
(2)令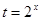 ,则
,则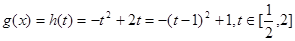 ,………………8分
,………………8分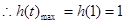 ,………………9分
,………………9分
又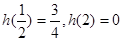 ,
,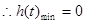 ,………………11分
,………………11分
即函数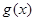 在
在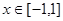 的上值域为
的上值域为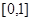 。………………12分
。………………12分
考点:本题主要考查函数的概念,指数函数的性质及其应用,二次函数图象和性质。
点评:典型题,复合指数函数问题。(2)小题中,利用换元法转化得到二次函数,利用二次函数图象和性质得到值域。

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
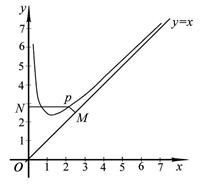
(本小题满分12分)探究函数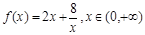 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数
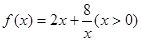 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数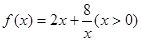 在区间 上递增.当
在区间 上递增.当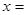 时,
时,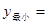 .
.(2)证明:函数
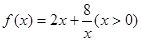 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
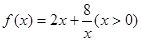 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明) 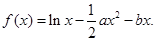
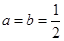 时,求函数
时,求函数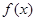 的最大值;
的最大值;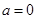 ,
,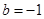 ,方程
,方程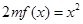 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 定义域为
定义域为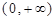 ,且
,且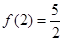 .
.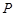 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点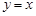 和
和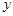 轴的垂线,垂足分别为
轴的垂线,垂足分别为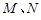 .
.
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)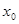 ,求
,求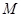 点的坐标(用
点的坐标(用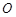 为坐标原点,求四边形
为坐标原点,求四边形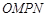 面积的最小值.(7分)
面积的最小值.(7分)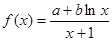 在点
在点 处的切线方程为
处的切线方程为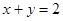 .
. ,
, 的值;
的值; 定义域内的任一个实数
定义域内的任一个实数 ,
,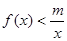 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.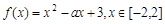 。
。 在
在 上的最小值是
上的最小值是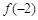 ,试解不等式
,试解不等式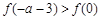 ;
;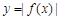 在
在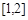 上单调递增,试求实数
上单调递增,试求实数 的取值范围。
的取值范围。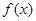 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当 ,且
,且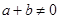 时有
时有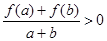 .
.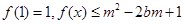 对所有
对所有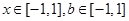 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 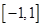 上的偶函数
上的偶函数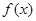 ,已知当
,已知当 时的解析式
时的解析式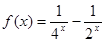
 在
在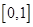 上的解析式;
上的解析式;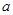 为非负实数,函数
为非负实数,函数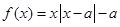 .
.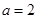 时,求函数的单调区间;
时,求函数的单调区间;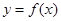 的零点个数.
的零点个数.