题目内容
(2008•海珠区一模)已知函数f(x)=x3+3ax-1
(1)若函数y=f(x)在x=-1时有与x轴平行的切线,求f(x)的表达式;
(2)设g(x)=
[af'(x)-3a2+3],其中f-1(x)是f(x)的导函数,若函数g(x)的图象与直线y=x相切,求a的值;
(3)设a=-m2,当实数m在什么范围内变化时,函数y=f(x)的图象与直线y=3只有一个公共点.
(1)若函数y=f(x)在x=-1时有与x轴平行的切线,求f(x)的表达式;
(2)设g(x)=
| 1 | 3 |
(3)设a=-m2,当实数m在什么范围内变化时,函数y=f(x)的图象与直线y=3只有一个公共点.
分析:(1)求导,根据函数y=f(x)的图象在x=-1时有与x轴平行的切线,利用导数的几何意义,可知f′(-1)=0,解方程即可求得结果;
(2)先求出函数g(x),再利用函数g(x)的图象与直线y=x相切,建立方程组,从而可求a的值
(3)先求f′(x)=3x2-3m2,再进行分类讨论:①当m=0时,f(x)=x3-1的图象与直线y=3只有一个公共点;②当m≠0时,求得极值,明确关键点,再利用图象间的关系求解.
(2)先求出函数g(x),再利用函数g(x)的图象与直线y=x相切,建立方程组,从而可求a的值
(3)先求f′(x)=3x2-3m2,再进行分类讨论:①当m=0时,f(x)=x3-1的图象与直线y=3只有一个公共点;②当m≠0时,求得极值,明确关键点,再利用图象间的关系求解.
解答:解:(1)f′(x)=3x2+3a
∵函数y=f(x)在x=-1时有与x轴平行的切线
∴f′(-1)=3+3a=0
∴a=-1
∴f(x)=x3-ax-1
(2)g(x)=
[af′(x)-3a2+3]=
[a(3x2+3a)-3a2+3]=ax2+1,
设函数g(x)=ax2+1与直线y=x的切点是P(x0,y0),
则有
,解得a=
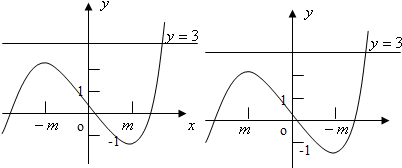
(3)f′(x)=3x2-3m2
①当m=0时,f(x)=x3-1的图象与直线y=3只有一个公共点
②当m≠0时,f(x)极小=f(|m|)=-2m2×|m|-1<-1
又∵f(x)的值域是R,且在(|m|,+∞)上单调递增
∴当x>|m|时函数y=f(x)的图象与直线y=3只有一个公共点.
当x<|m|时,恒有f(x)≤f(-|m|)
由题意得f(-|m|)<3
即2m2×|m|-1=2|m|3-1<3
解得m∈(-
,0)∪(0,
)
综上,m的取值范围是(-
,
)
∵函数y=f(x)在x=-1时有与x轴平行的切线
∴f′(-1)=3+3a=0
∴a=-1
∴f(x)=x3-ax-1
(2)g(x)=
| 1 |
| 3 |
| 1 |
| 3 |
设函数g(x)=ax2+1与直线y=x的切点是P(x0,y0),
则有
|
| 1 |
| 4 |
(3)f′(x)=3x2-3m2
①当m=0时,f(x)=x3-1的图象与直线y=3只有一个公共点
②当m≠0时,f(x)极小=f(|m|)=-2m2×|m|-1<-1
又∵f(x)的值域是R,且在(|m|,+∞)上单调递增
∴当x>|m|时函数y=f(x)的图象与直线y=3只有一个公共点.
当x<|m|时,恒有f(x)≤f(-|m|)
由题意得f(-|m|)<3
即2m2×|m|-1=2|m|3-1<3
解得m∈(-
| 3 | 2 |
| 3 | 2 |
综上,m的取值范围是(-
| 3 | 2 |
| 3 | 2 |

点评:本题考查导数的几何意义,考查利用导数研究函数的极值问题,考查数形结合的数学思想方法,同时考查灵活应用知识分析解决问题的能力和运算能力,属中档题.

练习册系列答案
相关题目
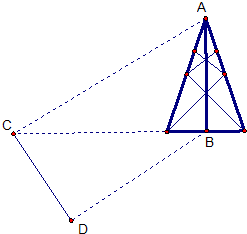 (2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB.
(2008•海珠区一模)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C测得塔顶A的仰角为30°,求塔高AB. (2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )
(2008•海珠区一模)如果一个几何体的三视图是如图所示(单位长度:cm则此几何体的表面积是( )