题目内容
已知函数 在点
在点 的切线方程为
的切线方程为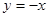
(1)求 的值;
的值;
(2)当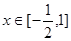 时,
时, 的图像与直线
的图像与直线 有两个不同的交点,求实数
有两个不同的交点,求实数 的取值范围;
的取值范围;
(3)证明对任意的正整数 ,不等式
,不等式 都成立.
都成立.
 在点
在点 的切线方程为
的切线方程为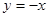
(1)求
 的值;
的值;(2)当
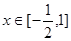 时,
时, 的图像与直线
的图像与直线 有两个不同的交点,求实数
有两个不同的交点,求实数 的取值范围;
的取值范围;(3)证明对任意的正整数
 ,不等式
,不等式 都成立.
都成立.(1)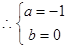 ;(2)
;(2)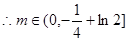 ;(3)见解析.
;(3)见解析.
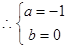 ;(2)
;(2)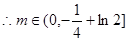 ;(3)见解析.
;(3)见解析.本试题主要考查了导数的几何意义的运用,以及运用导数求证不等式,和解决方程根的问题的综合运用。
解:(1)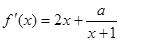 ……………………………1分
……………………………1分
由已知可得 ………………………………3分
………………………………3分
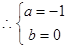 ……………………………………………………4分
……………………………………………………4分
(2)由(1)知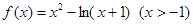

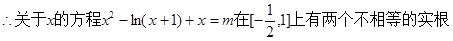 ……5分
……5分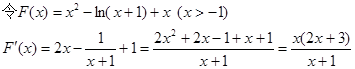
由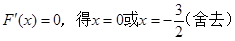
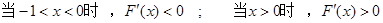
 ……………7分
……………7分
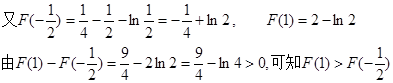
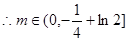 ………………………………………………9分
………………………………………………9分
(3)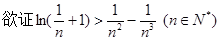
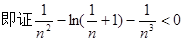
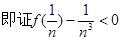 ……………………………………………………10分
……………………………………………………10分
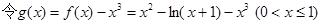
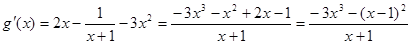

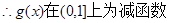
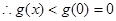 …………………………………………13分
…………………………………………13分
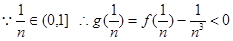
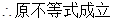 …………………………………………14分
…………………………………………14分
解:(1)
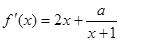 ……………………………1分
……………………………1分由已知可得
 ………………………………3分
………………………………3分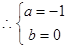 ……………………………………………………4分
……………………………………………………4分 (2)由(1)知
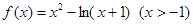

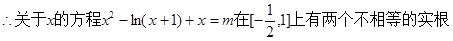 ……5分
……5分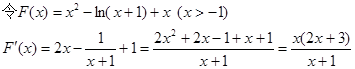
由
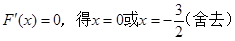
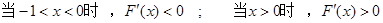
 ……………7分
……………7分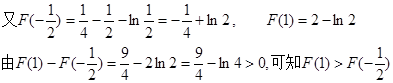
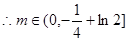 ………………………………………………9分
………………………………………………9分(3)
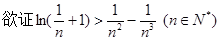
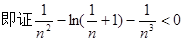
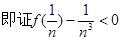 ……………………………………………………10分
……………………………………………………10分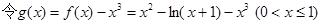
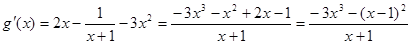

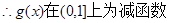
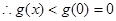 …………………………………………13分
…………………………………………13分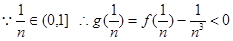
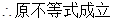 …………………………………………14分
…………………………………………14分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
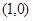 的直线与曲线
的直线与曲线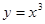 和
和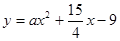 都相切,则
都相切,则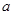 =_____.
=_____.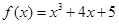 的图像在
的图像在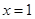 处的切线在x轴上的截距为( )
处的切线在x轴上的截距为( )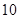
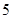
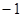
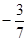
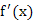 ,若函数
,若函数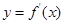 的图象关于直线
的图象关于直线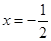 对称,且
对称,且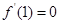 .](Ⅰ)求实数
.](Ⅰ)求实数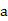 ,
,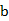 的值;(5分)(Ⅱ)求函数
的值;(5分)(Ⅱ)求函数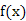 的极值
的极值 相切的切线方程为 .
相切的切线方程为 . ,且
,且 .
. 在
在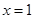 处取得极小值
处取得极小值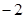 ,求函数
,求函数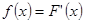 ,若
,若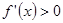 的解集为
的解集为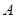 ,且满足
,且满足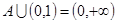 ,
,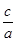 的取值范围。
的取值范围。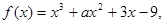 已知
已知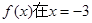 时取得极值,则a=( )
时取得极值,则a=( )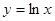 在点
在点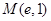 处的切线的方程为_______________;
处的切线的方程为_______________; 的单调递减区间为 .
的单调递减区间为 .