题目内容
已知点P(0,5)及圆C:x2+y2+4x-12y+24=0
(I)若直线l过点P且被圆C截得的线段长为4 ,求l的方程;
,求l的方程;
(II)求过P点的圆C的弦的中点D的轨迹方程
(1)直线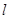 的方程为:
的方程为: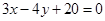 或
或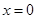 (2)
(2)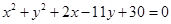
解析试题分析:(1)根据弦长和半径,可求出圆心到直线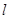 的距离为2 当直线的斜率存在时,设所求直线
的距离为2 当直线的斜率存在时,设所求直线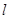 的方程为:
的方程为: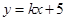 即
即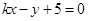 由点到直线的距离公式即可求出k的值,从而得直线
由点到直线的距离公式即可求出k的值,从而得直线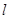 的方程 然后再考虑斜率不存在时的情况 (2)设过点P的圆C的弦的中点为
的方程 然后再考虑斜率不存在时的情况 (2)设过点P的圆C的弦的中点为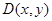 ,则
,则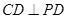 即
即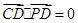 由此等式即可得中点D的轨迹方程 这属于利用等量关系求轨迹方程的问题
由此等式即可得中点D的轨迹方程 这属于利用等量关系求轨迹方程的问题
试题解析:(1)如图所示,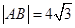 ,设
,设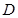 是线段
是线段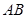 的中点,则
的中点,则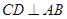
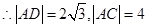 点C的坐标为(-2,6) 在
点C的坐标为(-2,6) 在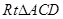 中,可得
中,可得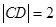
设所求直线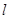 的方程为:
的方程为: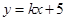 即
即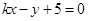
由点到直线的距离公式得: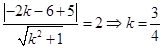
此时直线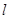 的方程为:
的方程为: 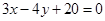 4分
4分
又直线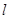 的斜率不存在时,也满足题意,此时方程为:
的斜率不存在时,也满足题意,此时方程为: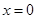
所以所求直线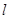 的方程为:
的方程为: 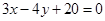 或
或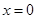 6分
6分
(2)设过点P的圆C的弦的中点为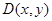 ,则
,则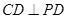 即
即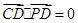
所以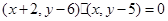 化简得所求轨迹的方程为:
化简得所求轨迹的方程为: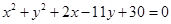 12分
12分
考点:1、直线与圆的方程;2、轨迹的方程

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
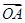 +
+ 与
与 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由. 的圆心在直线
的圆心在直线 上,且与
上,且与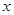 轴交于两点
轴交于两点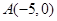 ,
,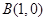 .
.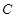
 的圆
的圆 ,点
,点 在圆
在圆 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹方程.
轨迹方程. )两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程.
)两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程. 与圆的位置关系。
与圆的位置关系。 到定点
到定点 与到定点
与到定点 的距离之比为
的距离之比为 .
. 的轨迹C的方程,并指明曲线C的轨迹;
的轨迹C的方程,并指明曲线C的轨迹; ,若曲线C上恰有三个点到直线
,若曲线C上恰有三个点到直线 的距离为1,求实数
的距离为1,求实数 的值。
的值。 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围。
的取值范围。 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆 与
与 轴的另一个交点为
轴的另一个交点为 .
. 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 ,
, 交于A、B两点;
交于A、B两点; 上的圆的方程.
上的圆的方程.