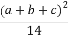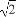题目内容
设0< a,b,c <1,求证:(1-a)b,(1-b)c,(1-c)a,不可能同时大于
.
见解析
【解析】证明：假设(1-a)b >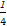
,(1-b)c >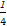,(1-c)a>,
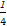则三式相乘:(1-a)b·(1-b)c·(1-c)a>
①.
又∵0< a,b,c <1,
∴0<(1-a)a≤[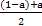
]2=.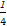
同理:(1-b)b≤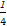,(1-c)c≤,
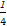以上三式相乘:
(1-a)a·(1-b)b·(1-c)c≤,
与①矛盾,
∴(1-a)b,(1-b)c,(1-c)a不可能同时大于.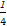
练习册系列答案
名校课堂系列答案
相关题目
