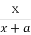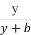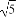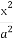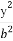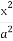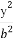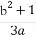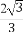题目内容
已知a,b,c为实数,且a+b+c+2-2m=0,a2+ b2+
b2+ c2+m-1=0.
c2+m-1=0.
(1)求证:a2+ b2+
b2+ c2≥
c2≥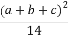 .
.
(2)求实数m的取值范围.
(1)见解析 (2) -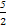 ≤m≤1
≤m≤1
【解析】(1)由柯西不等式得[a2+(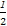 b)2+(
b)2+(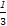 c)2](12+22+32)≥(a+b+c)2,
c)2](12+22+32)≥(a+b+c)2,
即(a2+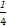 b2+
b2+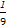 c2)×14≥(a+b+c)2,
c2)×14≥(a+b+c)2,
所以a2+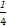 b2+
b2+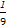 c2≥
c2≥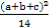 .
.
当且仅当|a|=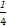 |b|=
|b|=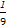 |c|时取得等号.
|c|时取得等号.
(2)由已知得a+b+c=2m-2,
a2+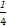 b2+
b2+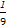 c2=1-m,
c2=1-m,
所以14(1-m)≥(2m-2)2,
即2m2+3m-5≤0.
所以-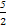 ≤m≤1.
≤m≤1.
又因为a2+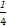 b2+
b2+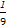 c2=1-m≥0,
c2=1-m≥0,
所以m≤1.所以-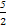 ≤m≤1.
≤m≤1.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目