题目内容
在某两个正数x,y之间,若插入一个数a,使x,a,y成等差数列,若插入两个数b,c,使x,b,c,y成等比数列,求证:(a+1)2≥(b+1)(c+1).
见解析
证明:方法一:由条件得
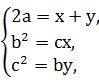
消去x,y即得:2a=
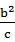 +
+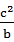 ,且有a>0,b>0,c>0,
,且有a>0,b>0,c>0,要证(a+1)2≥(b+1)(c+1),
只需证a+1≥
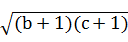 ,
,因为
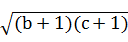 ≤
≤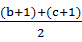 =
=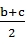 +1,
+1,所以只需证2a≥b+c,而2a=
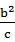 +
+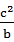 ,
,所以只需证
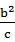 +
+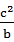 ≥b+c,
≥b+c,即b3+c3≥bc(b+c),(b+c)(b2+c2-bc)≥bc(b+c),
而b+c>0,则只需证b2+c2-bc≥bc,
即(b-c)2≥0,上式显然成立.
所以原不等式成立.
方法二:由等差、等比数列的定义知:
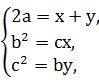
用x,y表示a,b,c得
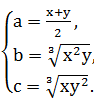
所以(b+1)(c+1)=(
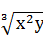 +1)(
+1)(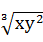 +1)
+1)≤
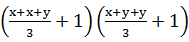
=
 (2x+y+3)(x+2y+3)
(2x+y+3)(x+2y+3)≤
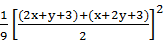
=
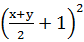 =(a+1)2,
=(a+1)2,所以原不等式成立.

练习册系列答案
相关题目
 ,且
,且 ,求
,求 的最小值.
的最小值. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。 的最小值是 .
的最小值是 . +1)
+1)
 <
< <b
<b