题目内容
在△ABC中,如果lga-lgc=lgsinB=-lg
并且B为锐角,试判断此三角形的形状特征.
| 2 |
在△ABC中,
∵lga-lgc=lgsinB=-lg
=lg
,并且B为锐角,
∴lg
=lgsinB=-lg
=lg
,
∴sinB=
,∴B=
,且
=
,
∴c=
a,∴cosB=
,
∴由余弦定理得cosB=
=
=
得a2=b2,即a=b,
∴三角形ABC为等腰三角形,
即A=B=
,
∴C=
,
故△ABC的形状等腰直角三角形,
∵lga-lgc=lgsinB=-lg
| 2 |
| ||
| 2 |
∴lg
| a |
| c |
| 2 |
| ||
| 2 |
∴sinB=
| ||
| 2 |
| π |
| 4 |
| a |
| c |
| ||
| 2 |
∴c=
| 2 |
| ||
| 2 |
∴由余弦定理得cosB=
| ||
| 2 |
| a2+c2-b2 |
| 2ac |
| 3a2-b2 | ||
2
|
得a2=b2,即a=b,
∴三角形ABC为等腰三角形,
即A=B=
| π |
| 4 |
∴C=
| π |
| 2 |
故△ABC的形状等腰直角三角形,

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
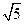 ,b=
,b=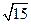 ,A=300,则边c= 。
,A=300,则边c= 。