题目内容
设椭圆上存在一点P,它到椭圆中心和长轴一个端点的连线互相垂直,求椭圆离心率的取值范围.
 <e<1.
<e<1.设椭圆方程为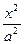 +
+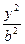 =1(a>b>0),A为右顶点(a,0)、P(x0,y0),
=1(a>b>0),A为右顶点(a,0)、P(x0,y0),
∵PO⊥PA,
∴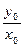 ·
· =-1,即y02=ax0-x02.
=-1,即y02=ax0-x02.
又 +
+ =1,
=1,
∴(a2-b2)x02-a3x0+a2b2=0,(x0-a)[(a2-b2)x0-ab2]=0.
又0<x0<a,∴x0=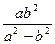 ,且0<
,且0<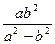 <a.而b2=a2-c2,
<a.而b2=a2-c2,
∴0<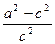 <1.
<1.
∴0<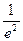 -1<1.
-1<1.
∴ <e<1.
<e<1.
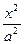 +
+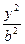 =1(a>b>0),A为右顶点(a,0)、P(x0,y0),
=1(a>b>0),A为右顶点(a,0)、P(x0,y0),∵PO⊥PA,
∴
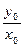 ·
· =-1,即y02=ax0-x02.
=-1,即y02=ax0-x02.又
 +
+ =1,
=1,∴(a2-b2)x02-a3x0+a2b2=0,(x0-a)[(a2-b2)x0-ab2]=0.
又0<x0<a,∴x0=
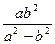 ,且0<
,且0<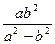 <a.而b2=a2-c2,
<a.而b2=a2-c2,∴0<
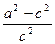 <1.
<1.∴0<
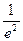 -1<1.
-1<1.∴
 <e<1.
<e<1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
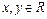 ,
,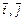 为直角坐标平面内x轴.y轴正方向上的单位向量,若
为直角坐标平面内x轴.y轴正方向上的单位向量,若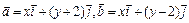 ,且
,且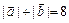
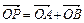 ,则OAPB为矩形,试求AB方程.
,则OAPB为矩形,试求AB方程. +y2=1中斜率为1的平行弦的中点的轨迹方程是_________________.
+y2=1中斜率为1的平行弦的中点的轨迹方程是_________________.

 -
-
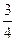
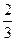
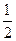
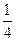
 +y2=1上一点P到右焦点F的距离为
+y2=1上一点P到右焦点F的距离为 ,则P到左准线的距离为________________.
,则P到左准线的距离为________________. =1表示焦点在y轴上的椭圆,则m的取值范围是( )
=1表示焦点在y轴上的椭圆,则m的取值范围是( )