题目内容
13.已知正项数列{an}与数列{bn}满足:a1=b1∈(0,2],$\frac{{b}_{n}}{{a}_{n}}$=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n-1}}$(n≥2,n∈N*).
若(1+$\frac{1}{{b}_{1}}$)(1+$\frac{1}{{b}_{2}}$)…(1+$\frac{1}{{b}_{n}}$)≥λ($\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$)(n∈N*),
则实数λ的最大值为1.
分析 由条件将n换为n+1,推得$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\frac{{b}_{n}}{{a}_{n}}$+$\frac{1}{{a}_{n}}$,再将含λ的不等式,化简整理,可得λ≤1+b1,由b1∈(0,2],可得λ的最大值.
解答 解:n≥2时,
∵$\frac{{b}_{n}}{{a}_{n}}$=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n-1}}$(n≥2,n∈N*),
∴$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n-1}}$+$\frac{1}{{a}_{n}}$,
∴$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\frac{{b}_{n}}{{a}_{n}}$+$\frac{1}{{a}_{n}}$,
∴bn+1an-(bn+1)an+1=0(n≥2且n∈N*),
所以$\frac{{b}_{n}+1}{{b}_{n+1}}$=$\frac{{a}_{n}}{{a}_{n+1}}$(n≥2且n∈N*),
∴(1+$\frac{1}{{b}_{1}}$)(1+$\frac{1}{{b}_{2}}$)…(1+$\frac{1}{{b}_{n}}$)=$\frac{1+{b}_{1}}{{b}_{1}}$•$\frac{1+{b}_{2}}{{b}_{2}}$•…•$\frac{1+{b}_{n}}{{b}_{n}}$
=$\frac{1}{{b}_{1}}$•$\frac{1+{b}_{1}}{{b}_{2}}$•$\frac{1+{b}_{2}}{{b}_{3}}$•…•$\frac{1+{b}_{n-1}}{{b}_{n}}$•$\frac{1+{b}_{n}}{{b}_{n+1}}$•bn+1
=$\frac{1}{{b}_{1}}$•$\frac{1+{b}_{1}}{{b}_{2}}$•$\frac{{a}_{2}}{{a}_{3}}$•…$\frac{{a}_{n-1}}{{a}_{n}}$•$\frac{{a}_{n}}{{a}_{n+1}}$•bn+1
=$\frac{1+{b}_{1}}{{b}_{1}}$•$\frac{{a}_{2}}{{b}_{2}}$•$\frac{{b}_{n+1}}{{a}_{n+1}}$=$\frac{{a}_{1}}{{b}_{1}}$(1+b1)($\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$)=(1+b1)($\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$),
由1+b1∈(1,3],
故λ≤1,λ的最大值为1.
故答案为:1.
点评 本题考查数列不等式恒成立问题的解法,考查累乘法的运用,考查运算求解能力,具有一定的难度.

| A. | (-∞,-1] | B. | [1,+∞) | C. | (1,+∞) | D. | (-∞,-1]∪[1,+∞) |
| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
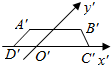 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.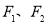 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过 的直线交椭圆于A、B两点若
的直线交椭圆于A、B两点若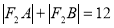 ,则
,则 =_____.
=_____.