题目内容
D,E是平行四边形OACB的对角线AB的三等分点(D靠近A),设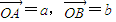 .
.(1)用
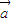 ,
,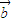 表示
表示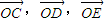 ;
;(2)证明:
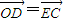 .
.
【答案】分析:(1)根据向量的加、减法法则和线性运算性质,不难得出用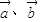 表示
表示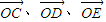 的式子;
的式子;
(2)由向量的减法法则得 =
=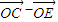 ,结合(1)的结论算出
,结合(1)的结论算出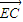 =
=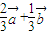 ,即可证出
,即可证出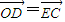 .
.
解答: 解:(1)根据向量加法的平行四边形法则,
解:(1)根据向量加法的平行四边形法则,
可得 =
=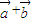
∵D是AB的三等分点(D靠近A),
∴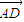 =
=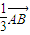 =
= =
= (
(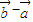 )
)
因此,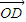 =
=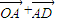 =
=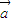 +
+ (
( )=
)=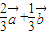
同理可得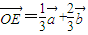
(2)∵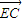 =
=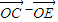 ,由(1)得
,由(1)得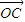 =
=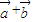 ,
,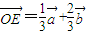
∴ =
=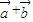 -(
-(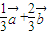 )=
)=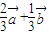
因此, =
=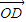 =
=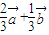 ,命题得证.
,命题得证.
点评:本题给出平行四边形,求用向量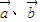 表示其它一些向量的式子,并求证向量相等.着重考查了平面向量的加法、减法法则和向量线性运算等知识,属于基础题.
表示其它一些向量的式子,并求证向量相等.着重考查了平面向量的加法、减法法则和向量线性运算等知识,属于基础题.
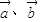 表示
表示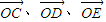 的式子;
的式子;(2)由向量的减法法则得
 =
=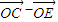 ,结合(1)的结论算出
,结合(1)的结论算出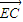 =
=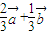 ,即可证出
,即可证出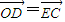 .
.解答:
 解:(1)根据向量加法的平行四边形法则,
解:(1)根据向量加法的平行四边形法则,可得
 =
=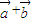
∵D是AB的三等分点(D靠近A),
∴
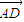 =
=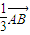 =
= =
= (
(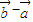 )
)因此,
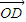 =
=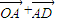 =
=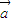 +
+ (
( )=
)=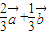
同理可得
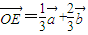
(2)∵
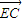 =
=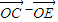 ,由(1)得
,由(1)得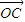 =
=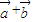 ,
,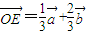
∴
 =
=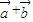 -(
-(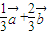 )=
)=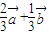
因此,
 =
=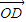 =
=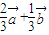 ,命题得证.
,命题得证.点评:本题给出平行四边形,求用向量
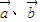 表示其它一些向量的式子,并求证向量相等.着重考查了平面向量的加法、减法法则和向量线性运算等知识,属于基础题.
表示其它一些向量的式子,并求证向量相等.着重考查了平面向量的加法、减法法则和向量线性运算等知识,属于基础题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
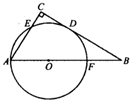 (2012•大连二模)任选一题作答选修:几何证明选讲如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(2012•大连二模)任选一题作答选修:几何证明选讲如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
 .
.