题目内容
设O为坐标原点，A（4，a），B（b，8），C（a，b），
（1）若四边形OABC是平行四边形，求∠AOC的大小；
（2）在（1）的条件下，设AB中点为D，OD与AC交于E，求
．
解：（1）由题意得：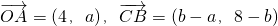
，
∵四边形OABC是平行四边形，∴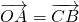
得
．
，
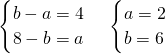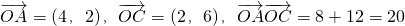又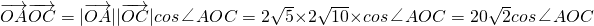
∴
．
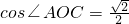∵0°＜∠AOC＜180°，∴∠AOC=45°．
（2）∵为AB中点，∴D的坐标为（5，5），
又由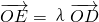
，故E的坐标为（5λ，5λ）．
∴
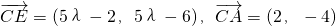
∵A，E，C三点共线，∴
．
得-4×（5λ-2）=（5λ-6）×2，解得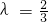
，从而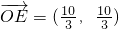
．
分析：（1）利用向量相等即可得出；
（2）利用中点坐标公式、向量共线的充要条件即可得出．
点评：熟练掌握向量相等、中点坐标公式、向量共线的充要条件是解题的关键．
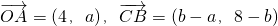，∵四边形OABC是平行四边形，∴
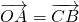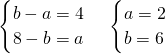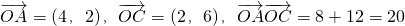得．，又
∴
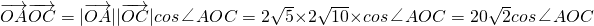
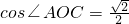．∵0°＜∠AOC＜180°，∴∠AOC=45°．
（2）∵为AB中点，∴D的坐标为（5，5），
又由
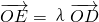，故E的坐标为（5λ，5λ）．∴
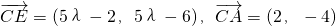
∵A，E，C三点共线，∴
．得-4×（5λ-2）=（5λ-6）×2，解得
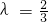，从而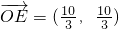．分析：（1）利用向量相等即可得出；
（2）利用中点坐标公式、向量共线的充要条件即可得出．
点评：熟练掌握向量相等、中点坐标公式、向量共线的充要条件是解题的关键．
练习册系列答案
相关题目