题目内容
设O是平行四边形ABCD两对角线的交点,P,Q,M,N分别是线段OA,OB,OC,OD的中点,在A,P,M,C中任取一点记为E,在B,Q,N,D中任取一点记为F,设
=
+
,则点G落在平行四边形ABCD外(不含边界)的概率是( )
| OG |
| OE |
| OF |
分析:列举出所有G点的个数,及落在平行四边形ABCD不含边界)的G点的个数,再将其代入古典概型计算公式进行求解.
解答: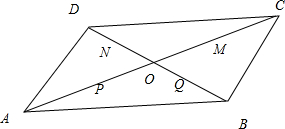 解:由题意知,G点的位置受到E、F点取法不同的限制,令(E,F)表示E、F的一种取法,则
解:由题意知,G点的位置受到E、F点取法不同的限制,令(E,F)表示E、F的一种取法,则
(A,B),(A,Q),(A,N),(A,D)
(P,B),(P,Q),(P,N),(P,D)
(M,B),(M,Q),(M,N),(M,D)
(C,B),(C,Q),(C,N),(C,D)共有16种取法,
而只有(P,Q),(P,N),(M,Q),(M,N)落在平行四边形内,故符合要求的G的只有4个,
落在平行四边形ABCD外(不含边界)的概率P=
=
故选C
 解:由题意知,G点的位置受到E、F点取法不同的限制,令(E,F)表示E、F的一种取法,则
解:由题意知,G点的位置受到E、F点取法不同的限制,令(E,F)表示E、F的一种取法,则(A,B),(A,Q),(A,N),(A,D)
(P,B),(P,Q),(P,N),(P,D)
(M,B),(M,Q),(M,N),(M,D)
(C,B),(C,Q),(C,N),(C,D)共有16种取法,
而只有(P,Q),(P,N),(M,Q),(M,N)落在平行四边形内,故符合要求的G的只有4个,
落在平行四边形ABCD外(不含边界)的概率P=
| 16-4 |
| 16 |
| 3 |
| 4 |
故选C
点评:本题主要考查古典概型公式的应用,解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
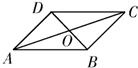 如图,设O是平行四边形ABCD的两条对角线AC,BD的交点,下列向量组:
如图,设O是平行四边形ABCD的两条对角线AC,BD的交点,下列向量组: