Question

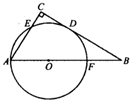（2012•大连二模）任选一题作答选修：几何证明选讲如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．
（I）若AC=6，AB=10，求⊙O的半径；
（Ⅱ）连接OE、ED、DF、EF．若四边形BDEF是平行四边形，试判断四边形OFDE的形状，并说明理由．

Answer 1

分析：（Ⅰ）连接OD． 设⊙O的半径为r，根据切线的性质及∠C=90°，可得OD∥AC，进而△OBD∽△ABC，进而根据相似三角形对应边成比例，构造关于r的方程，可得答案．
（II）由四边形BDEF是平行四边形，可证得OD=OE=DE=OF，进而根据菱形的判定定理，得到四边形OFDE为菱形．

解答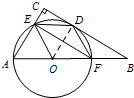：解：（Ⅰ）连接OD． 设⊙O的半径为r．
∵BC切⊙O于点D，
∴OD⊥BC．
又∵∠C=90°，
∴OD∥AC，
∴△OBD∽△ABC．
∴

OD

AC

=

OB

AB

，即 

r

6

=

10-r

10

．  
解得r=

15

4

，
∴⊙O的半径为

15

4

． …（4分）
（Ⅱ）结论：四边形OFDE是菱形． 理由如下 …（5分）
证明：∵四边形BDEF是平行四边形，
∴∠DEF=∠B．
∵∠DEF=

1

2

∠DOB，
∴∠B=

1

2

∠DOB．
∵∠ODB=90°，
∴∠DOB+∠B=

3

2

∠DOB=90°，
∴∠DOB=60°．
∵在平行四边形BDEF中，DE∥AB，
∴∠ODE=∠DOB=60°．
∵半径OD=OE，
∴△ODE是等边三角形．
∴OD=DE=OF，
即四边形OFDE的对边DE与OF平行且相等
∴四边形OFDE是平行四边形．
又∵邻边OE=OF，
∴平行四边形OFDE是菱形． …（10分）

点评：本题考查的知识点是切线的性质，三角形相似的判定与性质，平行四边形的性质与判定，难度不大，属于基础题．