题目内容
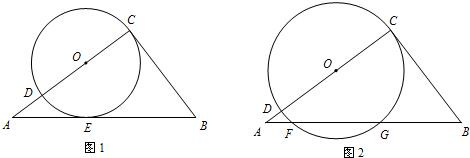
已知以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
(1)如图,求证:DE是⊙O的切线;
(2)连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAE的值.
思路解析:抓住各角度之间的联系进行转化.

(1)证明:连结OD、DB,
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠CDB=90°.
∵E为BC边上的中点,
∴CE=EB=DE.
∴∠1=∠2.
∵OB=OD,∴∠3=∠4.
∴∠1+∠4=∠2+∠3.
∵在Rt△ABC中,∠ABC=∠2+∠3=90°,∴∠EDO=∠1+∠4=90°.
∵D为⊙O上的点,
∴DE是⊙O的切线.
(2)解:∠CAB=45°,sin∠CAE=![]() .
.

练习册系列答案
相关题目
 (A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为
(A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为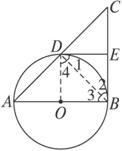
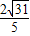 ,求⊙O的半径.
,求⊙O的半径.