题目内容
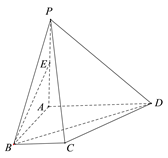
【题目】如图,已知椭圆![]() 与椭圆
与椭圆![]() 的离心率相同.
的离心率相同.

(1)求![]() 的值;
的值;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,交椭圆
,交椭圆![]() 于另一点
于另一点![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 之间).①求
之间).①求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点);②设
为坐标原点);②设![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试探究点
,试探究点![]() 是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②点
;②点![]() 在定直线
在定直线![]() 上
上
【解析】
(1)利用两个椭圆离心率相同可构造出方程,解方程求得结果;(2)①当![]() 与
与![]() 轴重合时,可知不符合题意,则可设直线
轴重合时,可知不符合题意,则可设直线![]() 的方程:
的方程:![]() 且
且![]() ;设
;设![]() ,
,![]() ,联立直线
,联立直线![]() 与椭圆
与椭圆![]() 方程可求得
方程可求得![]() ,则可将所求面积表示为:
,则可将所求面积表示为:![]() ,利用换元的方式将问题转化为二次函数的最值的求解,从而求得所求的最大值;②利用中点坐标公式求得
,利用换元的方式将问题转化为二次函数的最值的求解,从而求得所求的最大值;②利用中点坐标公式求得![]() ,则可得直线
,则可得直线![]() 的方程;联立直线
的方程;联立直线![]() 与椭圆
与椭圆![]() 方程,从而可求解出
方程,从而可求解出![]() 点坐标,进而得到直线
点坐标,进而得到直线![]() 方程,与直线
方程,与直线![]() 联立解得
联立解得![]() 坐标,从而可得定直线.
坐标,从而可得定直线.
(1) 由椭圆![]() 方程知:
方程知:![]() ,
,![]()
![]()
![]() 离心率:
离心率: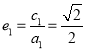
又椭圆![]() 中,
中,![]() ,
,![]()
![]()
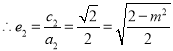 ,又
,又![]() ,解得:
,解得:![]()
(2)①当直线![]() 与
与![]() 轴重合时,
轴重合时,![]() 三点共线,不符合题意
三点共线,不符合题意
故设直线![]() 的方程为:
的方程为:![]() 且
且![]()
设![]() ,
,![]()
由(1)知椭圆![]() 的方程为:
的方程为:![]()
联立方程消去![]() 得:
得:![]()
即:![]()
解得:![]() ,
,![]() ,
,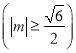
又![]()
令![]()
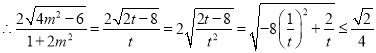 ,此时
,此时![]()
![]() 面积的最大值为:
面积的最大值为:![]()
②由①知:![]()
![]()
![]()
![]() 直线
直线![]() 的斜率:
的斜率:![]()
则直线![]() 的方程为:
的方程为:![]()
联立方程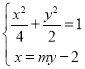 消去
消去![]() 得:
得:![]() ,解得:
,解得:![]()
![]()
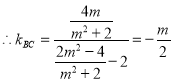
则直线![]() 的方程为:
的方程为:![]()
联立直线![]() 和
和![]() 的方程
的方程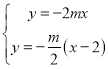 ,解得:
,解得:![]()
![]() 点
点![]() 在定直线
在定直线![]() 上运动
上运动

 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
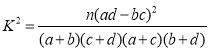
【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
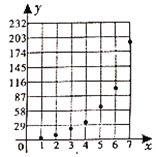
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: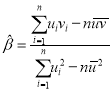 ,
,![]() 。
。
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: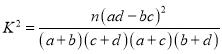
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |