题目内容
【题目】某工厂的某种产品成箱包装，每箱20件，每一箱产品在交付用户时，用户要对该箱中部分产品作检验.设每件产品为不合格品的概率都为
，且各件产品是否合格相互独立.
（1）记某一箱20件产品中恰有2件不合格品的概率为
，取最大值时对应的产品为不合格品概率为
，求；
（2）现从某一箱产品中抽取3件产品进行检验，以（1）中确定的作为p的值，已知每件产品的检验费用为10元，若检验出不合格品，则工厂要对每件不合格品支付30元的赔偿费用，检验费用与赔偿费用的和记为
，求的分布列和数学期望.
【答案】（1）
；（2）分布列见解析；
.
【解析】
（1）根据二项分布概率公式可得
，利用导数可确定单调性，从而得到最大值点；
（2）首先确定
所有可能的取值和对应的概率，由此得到分布列；根据数学期望计算公式计算可得期望.
（1）
件产品中恰有
件不合格品的概率
，
，
令
，又
，解得：
，
当
时，
；当
时，
；
在
上单调递增，在
上单调递减，
当时，取得最大值，即.
（2）由题意得：所有可能的取值为：
，
，
，
，
；
；
；
；
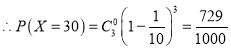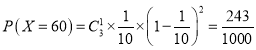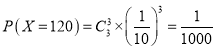的分布列为：
|
|
|
|
|
|
|
|
|
|
数学期望
.
练习册系列答案
相关题目
