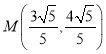题目内容
【题目】如图所示,一张形状为等边三角形![]() 的纸片,边长为8,将它对折,使顶点
的纸片,边长为8,将它对折,使顶点![]() 落在边
落在边![]() 上,当点
上,当点![]() 沿着
沿着![]() 从点
从点![]() 到点
到点![]() 移动时,求折痕长的最大值及最小值.
移动时,求折痕长的最大值及最小值.
【答案】最大值为![]() ,最小值为4
,最小值为4
【解析】
设![]() ,根据对称性只需考虑
,根据对称性只需考虑![]() .由正弦定理可得
.由正弦定理可得![]() (用
(用![]() 表示),从而可得
表示),从而可得![]() ,类比可得
,类比可得![]() ,即得折痕
,即得折痕![]() 函数关系式,再化简
函数关系式,再化简![]() 得
得![]() ,根据三角函数单调性确定折痕
,根据三角函数单调性确定折痕![]() 函数单调性,最后根据单调性求最值.
函数单调性,最后根据单调性求最值.
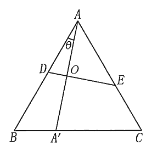
解 设对折后点![]() 落在
落在![]() 上的点为
上的点为![]() ,折痕为
,折痕为![]() 交
交![]() 于点
于点![]() ,则
,则![]() 是
是![]() 的中垂线,设
的中垂线,设![]() ,由等边三角形的对称性可知,我们只需考虑
,由等边三角形的对称性可知,我们只需考虑![]() .
.
在![]() 中,由正弦定理,得
中,由正弦定理,得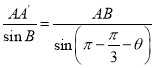 ,即
,即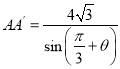 .
.
在![]() 与
与![]() 中,
中,
![]() ,
,
![]() .
.

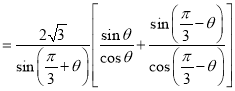
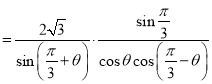 .
.
考察分母中的![]() .
.
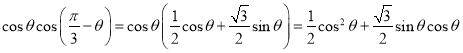
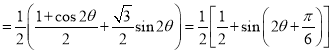 .
.
当![]() 时,
时,![]() ,
,
所以![]() 是递增函数且
是递增函数且![]() 也是递增函数.
也是递增函数.
因为它们的函数值均为正,所以![]() 在
在![]() 递增.
递增.
当![]() 时,
时,![]() 取最大值为
取最大值为![]() .当
.当![]() 时,
时,![]() 取最小值为4.
取最小值为4.
所以折痕长的最大值为![]() ,最小值为4.
,最小值为4.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目