题目内容
(本小题满分14分)
已知数列{an},且x=![]() 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求数列{an}的通项公式;
(2)记bn=2(1-![]() ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
(3)若cn=![]() ,证明:
,证明:![]() ( n∈N﹡).
( n∈N﹡).
解:(1)f ′(x)=3an-1x2-3[(t+1)an-an+1],
所以f ′(![]() )=3an-1t-3[(t+1)an-an+1]=0.
)=3an-1t-3[(t+1)an-an+1]=0.
整理得:an+1-an=t(an-an-1) .…………………………………………2分
当 t=1时,{an-an-1}是常数列,得![]() ;
;
当 t≠1时{an-an-1}是以 a2-a1=t2-t为首项, t为公比的等比数列,
所以 an-an-1=(t2-t)·t n-2=(t-1)·t n-1.
方法一:由上式得
(an-an-1)+(an-1-an-2)+…+(a2-a1)=(t-1)(tn-1+tn-2+…+t),
即 an-a1=(t-1)·![]() =tn-t,
=tn-t,
所以 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .………………………4分
方法二:由上式得: an-tn=an-1-tn-1,
所以{an-tn}是常数列,an-tn=a1-t=0 an=tn(n≥2) .
又,当t=1时上式仍然成立,故 an=tn(n∈N﹡) .
(2)当t=2, bn=![]() =2-
=2-![]() .
.
∴Sn=2n-(1+![]() +
+![]() +…+
+…+![]() )=2n-
)=2n-![]()
=2n-2(1-![]() )=2n-2+2·
)=2n-2+2·![]()
由Sn>2010,得
2n-2+2(![]() )n>2010, n+(
)n>2010, n+(![]() )n>1006,
)n>1006,
当n≤1005时, n+(![]() )n<1006,
)n<1006,
当 n≥1006时, n+(![]() )n>1006,
)n>1006,
因此 n的最小值为1006.………………………………………………8分
(3)cn=![]() 且c1=
且c1=![]() ,所以
,所以
![]() .
.
因为![]() =
= =
=
= ≥
≥![]() ,
,
所以
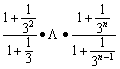 =
= .
.
从而原命题得证.…………………………………………………………14分

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)