题目内容
【题目】已知函数f(x)=x2﹣(a+1)x+b.
(1)若f(x)<0的解集为(﹣1,3),求a,b的值;
(2)当a=1时,若对任意x∈R,f(x)≥0恒成立,求实数b的取值范围;
(3)当b=a时,解关于x的不等式f(x)<0(结果用a表示).
【答案】
(1)解:∵f(x)<0的解集是(﹣1,3),
∴x2﹣(a+1)x+b=0的两个根是﹣1,3,
∴ 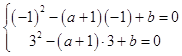 ,
,
解得:a=1,b=﹣3;
(2)解:a=1时,f(x)=x2﹣2x+b,
∵x∈R,f(x)≥0恒成立,
∴△=(﹣2)2﹣4b≤0,解得:b≥1,
故b的范围是[1,+∞);
(3)解:b=a时,f(x)<0即x2﹣(a+1)x+a<0,
∴(x﹣1)(x﹣a)<0,
a<1时,a<x<1,a=1时,x∈,
a>1时,1<x<a,
综上,a<1时,不等式f(x)<0的解集是{x|a<x<1},
a=1时,不等式f(x)<0的解集是,
a>1时,不等式f(x)<0的解集是{x|1<x<a}.
【解析】(1)将x=﹣1,3代入f(x)=0,得到关于a,b的方程组,解出即可;(2)将a=1代入函数的解析式,根据二次函数的性质求出b的范围即可;(3)问题转化为x2﹣(a+1)x+a<0,即(x﹣1)(x﹣a)<0,通过讨论a的范围求出不等式的解集即可.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
