题目内容
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 =bx+a;
=bx+a;(2)试预测加工10个零件需要多少时间?
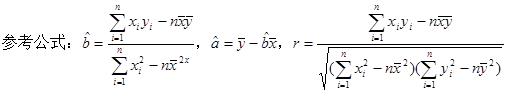
| n-2 | 1 | 2 | 3 | 4 |
| 小概率0.05 | 0.997 | 0.950 | 0.878 | 0.811 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 |
(1) y=0.7x+1.05 (2)8.05
解析试题分析:(1)由表中数据得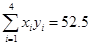
 =3.5,
=3.5,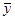 =3.5,
=3.5,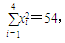
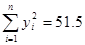
作统计假设:x与y不具有线性相关关系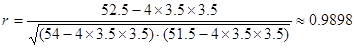
 ,故有95%把我认为x与y之间具有线性相关关系.
,故有95%把我认为x与y之间具有线性相关关系.
由数据得b=0.7.∴a=1.05.
∴回归直线方程为:y=0.7x+1.05.
(2)将x=10代入回归直线方程得,y=0.7×10+1.05=8.05
∴预测加工10个零件需要8.05小时.
考点:回归方程及线性相关性的判定
点评:本题思路简单,主要是将数据代入相应的公式计算,要求在数据处理时认真细心即可

练习册系列答案
相关题目
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y (件 ) | 90 | 84 | 83 | 80 | 75 | 68 |
 与单价
与单价 间的回归直线方程;
间的回归直线方程;(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
某种产品的广告费支出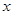 与销售额
与销售额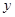 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s;
 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高; ,
, ,
, ,
, )
)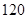 人,其中女性
人,其中女性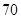 人,男性
人,男性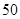 人.女性中有
人.女性中有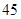 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外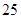 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外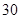 人主要的休闲方式是运动.
人主要的休闲方式是运动.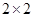 的列联表;
的列联表;