题目内容
10.已知函数f(x)=ex-ax有且只有一个零点,则实数a的取值范围为(-∞,0)∪{e}.分析 函数f(x)=ex-ax有且只有一个零点可转化为函数y=ex与y=ax的图象有且只有一个交点;作函数图象可知,分相切与不相切讨论即可.
解答 解:∵函数f(x)=ex-ax有且只有一个零点,
∴函数y=ex与y=ax的图象有且只有一个交点,
作函数y=ex与y=ax的图象如下,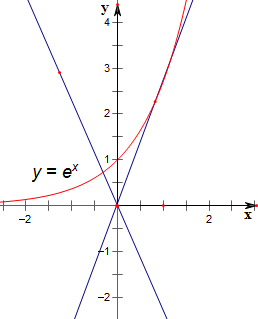
结合图象知,当a<0时成立,
当a>0时,相切时成立,
故(ex)′=ex=$\frac{{e}^{x}-0}{x-0}$;
故x=1;
故a=e;
综上所述,实数a的取值范围为(-∞,0)∪{e}.
故答案为:(-∞,0)∪{e}.
点评 本题考查了学生作图与用图的能力,同时考查了导数的几何意义的应用,属于中档题.

练习册系列答案
相关题目
20.cos240°=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
18.已知等比数列{an}的公比为正数,且a2=1,a3•a9=2a52,则a1等于( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
19.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-2(x≥0)}\\{-1-\frac{1}{2}{x}^{2(x<0)}}\end{array}\right.$,若关于x的方程f(x)-mx=0恰有3个不同的实数根,则实数m的取值范围为( )
| A. | (-∞,$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (0,$\sqrt{2}$) | D. | (1,+∞) |
20.已知a,b为正实数,则“a>1且b>1”是“ab>1”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |