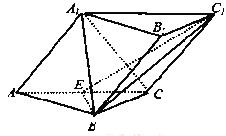
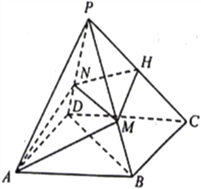
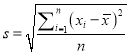ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼ŹĒijŹŠ3ŌĀ1ČÕÖĮ14ČÕµÄæÕĘųÖŹĮæÖøŹżĒ÷ŹĘĶ¼£®æÕĘųÖŹĮæÖøŹżŠ”ÓŚ100±ķŹ¾æÕĘųÖŹĮæÓÅĮ¼£¬æÕĘųÖŹĮæÖøŹż“óÓŚ200±ķŹ¾æÕĘųÖŲ¶ČĪŪČ¾£®Ä³ČĖĖ껜єŌń3ŌĀ1ČÕÖĮ3ŌĀ13ČÕÖŠµÄijŅ»Ģģµ½“ļøĆŹŠ£¬²¢Ķ£Įō2Ģģ£®
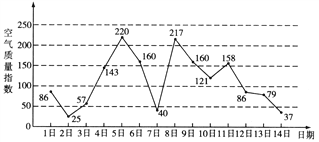
£Ø¢ń£©Ēó“ĖČĖµ½“ļµ±ČÕæÕĘųÖŲ¶ČĪŪČ¾µÄøÅĀŹ£»
£Ø¢ņ£©ÉčXŹĒ“ĖČĖĶ£ĮōĘŚ¼äæÕĘųÖŹĮæÓÅĮ¼µÄĢģŹż£¬ĒóXµÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū£»
£Ø¢ó£©ÓÉĶ¼ÅŠ¶Ļ“ÓÄÄĢģæŖŹ¼Į¬ŠųČżĢģµÄæÕĘųÖŹĮæÖøŹż·½²ī×ī“ó£æ£Ø½įĀŪ²»ŅŖĒóÖ¤Ć÷£©
”¾“š°ø”æ(¢ń) ![]() £»(¢ņ)“š°ø¼ū½āĪö£»(¢ó)“Ó3ŌĀ5ČÕæŖŹ¼Į¬ŠųČżĢģµÄæÕĘųÖŹĮæÖøŹż·½²ī×ī“ó.
£»(¢ņ)“š°ø¼ū½āĪö£»(¢ó)“Ó3ŌĀ5ČÕæŖŹ¼Į¬ŠųČżĢģµÄæÕĘųÖŹĮæÖøŹż·½²ī×ī“ó.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČČ·¶ØæÕĘųÖŲ¶ČĪŪČ¾ČÕ£¬ŌŁøł¾Ż¹ÅµäøÅŠĶøÅĀŹ¹«Ź½ĒóøÅĀŹĪŖ![]() £¬£Ø2£©ĻČČ·¶ØĖ껜±äĮæČ”·Ø£¬ŌŁ·Ö±šĒó¶ŌÓ¦øÅĀŹ£¬×īŗóøł¾ŻŹżŃ§ĘŚĶū¹«Ź½ĒóĘŚĶū£¬(3) ·½²ī×ī“󣬼“Źż¾Ż±ä»Æ·ł¶Č×ī“ó£¬ÓÉĶ¼æÉµĆ½įĀŪ.
£¬£Ø2£©ĻČČ·¶ØĖ껜±äĮæČ”·Ø£¬ŌŁ·Ö±šĒó¶ŌÓ¦øÅĀŹ£¬×īŗóøł¾ŻŹżŃ§ĘŚĶū¹«Ź½ĒóĘŚĶū£¬(3) ·½²ī×ī“󣬼“Źż¾Ż±ä»Æ·ł¶Č×ī“ó£¬ÓÉĶ¼æÉµĆ½įĀŪ.
ŹŌĢā½āĪö£ŗÉčAi±ķŹ¾ŹĀ¼ž”°“ĖČĖÓŚ3ŌĀiČÕµ½“ļøĆŹŠ”±£Øi=1£¬2£¬”£¬13£©£®
øł¾ŻĢāŅā£¬ ![]() £¬ĒŅ
£¬ĒŅ![]()
£Ø¢ń£©ÉčBĪŖŹĀ¼ž”°“ĖČĖµ½“ļµ±ČÕæÕĘųÖŲ¶ČĪŪČ¾”±£¬Ōņ![]() £®
£®
”ą![]()
£Ø¢ņ£©ÓÉĢāŅāæÉÖŖ£¬XµÄĖłÓŠæÉÄÜȔֵĪŖ0£¬1£¬2£¬ĒŅ
![]() £¬
£¬
![]()
![]()
”ąXµÄ·Ö²¼ĮŠĪŖ£ŗ
X | 0 | 1 | 2 |
P |
|
|
|
¹ŹXµÄŹżŃ§ĘŚĶū![]()
£Ø¢ó£©“Ó3ŌĀ5ČÕæŖŹ¼Į¬ŠųČżĢģµÄæÕĘųÖŹĮæÖøŹż·½²ī×ī“ó

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æĻÖŌŚµÄČĖ»ł±¾ĆæĢģ¶¼Ąė²»æŖŹÖ»ś£¬Šķ¶ąČĖŹÖ»śŅ»µ©²»ŌŚÉķ±ß¾Ķ²»Źę·ž£¬¼øŗõ“ļµ½ŹÖ»ś¶žŹ®ĖÄŠ”Ź±²»ĄėÉķ£¬ÕāĄąČĖČŗ±»³ĘĪŖ”°ŹÖ»śæŲ”±£¬ÕāŅ»ČŗĢåŌŚ“óѧɜ֊±Č½ĻĶ»³ö.ĪŖĮĖµ÷²é“óѧɜĆæĢģŹ¹ÓĆŹÖ»śµÄŹ±¼ä£¬Ä³µ÷²é¹«Ė¾Õė¶Ōijøߊ£ÄŠÉś”¢Å®Éśø÷25Ćūѧɜ½ųŠŠĮĖµ÷²é£¬ĘäÖŠĆæĢģŹ¹ÓĆŹÖ»śŹ±¼ä³¬¹ż8Š”Ź±µÄ±»³ĘĪŖ£ŗ”°ŹÖ»śæŲ”±£¬·ńŌņ±»³ĘĪŖ”°·ĒŹÖ»śæŲ”±.µ÷²é½į¹ūČēĻĀ£ŗ
ŹÖ»śæŲ | ·ĒŹÖ»śæŲ | ŗĻ¼Ę | |
Å®Éś | 5 | ||
ÄŠÉś | 10 | ||
ŗĻ¼Ę | 50 |
£Ø1£©½«ÉĻĆęµÄĮŠĮŖ±ķ²¹³äĶźÕū£¬ŌŁÅŠ¶ĻŹĒ·ńÓŠ99.5%µÄ°ŃĪÕČĻĪŖ”°ŹÖ»śæŲ”±ÓėŠŌ±šÓŠ¹Ų£¬ĖµĆ÷ÄćµÄĄķÓÉ£»
£Ø2£©ĻÖ“Ó±»µ÷²éµÄÄŠÉśÖŠ°“·Ö²ć³éŃłµÄ·½·ØŃ”³ö5ČĖ£¬ŌŁ“ÓÕā5ČĖÖŠĖ껜єȔ3ČĖ²Ī¼Ó׳Ģø»į£¬¼ĒÕā3ČĖÖŠ”°ŹÖ»śæŲ”±µÄČĖŹżĪŖ![]() £¬ŹŌĒó
£¬ŹŌĒó![]() µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū.
µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū.
²Īæ¼¹«Ź½£ŗ 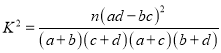 £¬ĘäÖŠ
£¬ĘäÖŠ![]() .
.
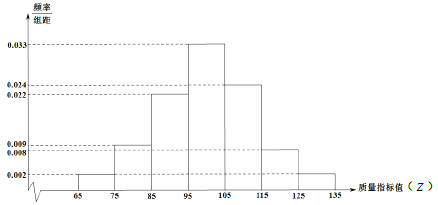
”¾ĢāÄæ”æøßæ¼ø“Ļ°¾¹ż¶žĀÖ”°¼ū¶ąŹ¶¹ć”±Ö®ŗó£¬ĪŖĮĖŃŠ¾ææ¼Ē°”°ĻŽŹ±ĒĄ·Ö”±Ēæ»ÆѵĮ·“ĪŹż![]() Óė“šĢāÕżČ·ĀŹ
Óė“šĢāÕżČ·ĀŹ![]() µÄ¹ŲĻµ£¬¶ŌijŠ£øßČżÄ³°ąŃ§Éś½ųŠŠĮĖ¹Ų×¢Ķ³¼Ę£¬µĆµ½Čē±ķŹż¾Ż£ŗ
µÄ¹ŲĻµ£¬¶ŌijŠ£øßČżÄ³°ąŃ§Éś½ųŠŠĮĖ¹Ų×¢Ķ³¼Ę£¬µĆµ½Čē±ķŹż¾Ż£ŗ
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
£Ø1£©Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄĻߊŌ»Ų¹é·½³Ģ£¬²¢Ō¤²ā“šĢāÕżČ·ĀŹŹĒ
µÄĻߊŌ»Ų¹é·½³Ģ£¬²¢Ō¤²ā“šĢāÕżČ·ĀŹŹĒ![]() µÄĒæ»ÆѵĮ·“ĪŹż£Ø±£ĮōÕūŹż£©£»
µÄĒæ»ÆѵĮ·“ĪŹż£Ø±£ĮōÕūŹż£©£»
£Ø2£©ČōÓĆ![]() £Ø
£Ø![]() £©±ķŹ¾Ķ³¼ĘŹż¾ŻµÄ”°Ēæ»Æ¾łÖµ”±£Ø±£ĮōÕūŹż£©£¬Čō”°Ēæ»Æ¾łÖµ”±µÄ±ź×¼²īŌŚĒų¼ä
£©±ķŹ¾Ķ³¼ĘŹż¾ŻµÄ”°Ēæ»Æ¾łÖµ”±£Ø±£ĮōÕūŹż£©£¬Čō”°Ēæ»Æ¾łÖµ”±µÄ±ź×¼²īŌŚĒų¼ä![]() ÄŚ£¬ŌņĒæ»ÆѵĮ·ÓŠŠ§£¬ĒėĪŹÕāøö°ąµÄĒæ»ÆѵĮ·ŹĒ·ńÓŠŠ§£æ
ÄŚ£¬ŌņĒæ»ÆѵĮ·ÓŠŠ§£¬ĒėĪŹÕāøö°ąµÄĒæ»ÆѵĮ·ŹĒ·ńÓŠŠ§£æ
ø½£ŗ»Ų¹éÖ±ĻߵĊ±ĀŹŗĶ½Ų¾ąµÄ×īŠ”¶ž³Ė·Ø¹Ą¼Ę¹«Ź½·Ö±šĪŖ£ŗ
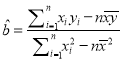 £¬
£¬ ![]() £¬Ńł±¾Źż¾Ż
£¬Ńł±¾Źż¾Ż![]() £¬
£¬ ![]() £¬”£¬
£¬”£¬ ![]() µÄ±ź×¼²īĪŖ
µÄ±ź×¼²īĪŖ