题目内容
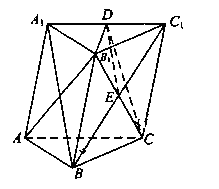
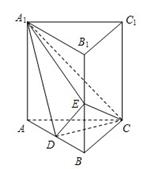
如图,棱柱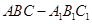 的侧面
的侧面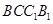 是菱形,
是菱形,

(Ⅰ)证明:平面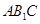
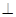 平面
平面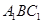 ;
;
(Ⅱ)设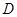 是
是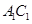 上的点,且
上的点,且 平面
平面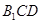 ,求
,求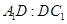 的值.
的值.
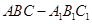 的侧面
的侧面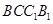 是菱形,
是菱形,

(Ⅰ)证明:平面
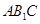
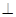 平面
平面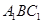 ;
;(Ⅱ)设
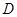 是
是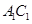 上的点,且
上的点,且 平面
平面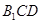 ,求
,求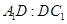 的值.
的值.(Ⅰ)详见解析;(Ⅱ)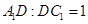
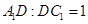
试题分析:(Ⅰ)由题中侧面
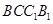 是菱形,可见它的对角线相互垂直,即
是菱形,可见它的对角线相互垂直,即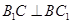 ,再加上所给的条件
,再加上所给的条件 ,这样就出现了一条直线同时与两条直线垂直,而这两条直线确定了要证的两个平面中一个平面,即平面
,这样就出现了一条直线同时与两条直线垂直,而这两条直线确定了要证的两个平面中一个平面,即平面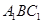 ,根据直线与平面垂直的判定定理可证得
,根据直线与平面垂直的判定定理可证得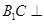 平面
平面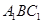 ,最后由平面与平面垂直的判定定理,可以得证; (Ⅱ)由(Ⅱ)中的条件
,最后由平面与平面垂直的判定定理,可以得证; (Ⅱ)由(Ⅱ)中的条件 平面
平面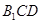 ,由直线与平面平行的性质定理,可构造出一个过
,由直线与平面平行的性质定理,可构造出一个过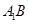 的平面,即为图中的平面
的平面,即为图中的平面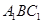 ,然后在
,然后在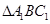 中,由菱形
中,由菱形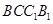 知
知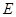 为一边中点,再结合三角形中位线不难得出
为一边中点,再结合三角形中位线不难得出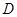 为
为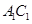 的中点,这样得到
的中点,这样得到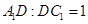
试题解析:解:(Ⅰ)因为侧面
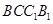 是菱形,所以
是菱形,所以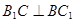
又已知
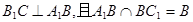
所又
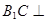 平面
平面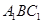 ,又
,又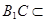 平面
平面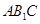 ,
,所以平面
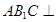 平面
平面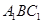 .
.(Ⅱ)设
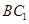 交
交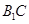 于点
于点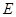 ,连结
,连结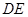 ,
,则
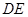 是平面
是平面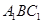 与平面
与平面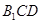 的交线,
的交线,因为
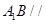 平面
平面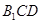 ,所以
,所以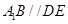 .
.又
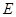 是
是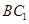 的中点,所以
的中点,所以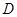 为
为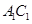 的中点.
的中点.即
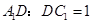 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
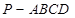 中,底面
中,底面 是直角梯形,
是直角梯形,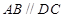 ,
,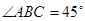 ,
,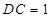 ,
,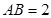 ,
,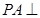 平面
平面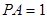 .
. 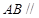 平面
平面 ;
; 平面
平面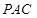 ;
;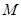 是
是 的中点,求三棱锥
的中点,求三棱锥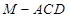 的体积.
的体积. 中,
中,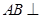 平面
平面 ,
,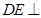 平面
平面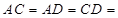
 ,
,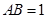 ,
,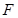 为
为 的中点.
的中点.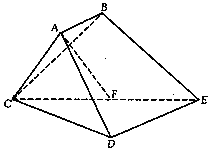
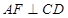 ;
;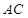 与平面
与平面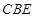 所成角的余弦值的大小.
所成角的余弦值的大小.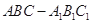 中,
中,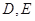 分别是
分别是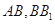 的中点,
的中点,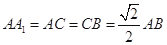 .
.
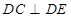 ;
;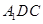 所成角的正弦值.
所成角的正弦值.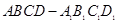 中,
中,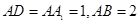 ,点E是AB的中点.
,点E是AB的中点.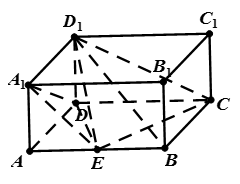
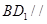 平面
平面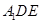 ;
;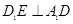 ;
;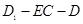 的正切值.
的正切值.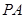 垂直于⊙
垂直于⊙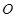 所在的平面,
所在的平面,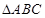 内接于⊙
内接于⊙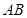 为⊙
为⊙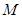 为线段
为线段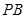 的中点.现有结论:①
的中点.现有结论:①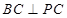 ;②
;② 平面
平面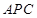 ;③点
;③点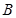 到平面
到平面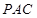 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )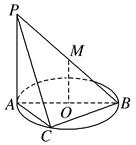
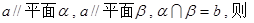
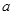 与
与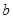 ( )
( )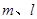 ,平面
,平面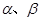 ,且
,且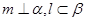 ,给出下列命题:
,给出下列命题: 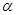 ∥
∥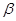 ,则m⊥
,则m⊥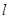 ; ②若
; ②若