题目内容
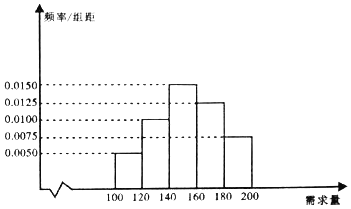
【题目】某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元；未售出的产品，每盒亏损30元
根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示，该同学为这个开学季购进了160盒该产品，以
单位：盒，
表示这个开学季内的市场需求量，
单位：元
表示这个开学季内经销该产品的利润
根据直方图估计这个开学季内市场需求量x的平均数和众数；
将y表示为x的函数；
根据直方图估计利润不少于4800元的概率．
【答案】（1）153,150（2）y=
,（3）0.9
【解析】
试题（1）以各组的中间值为各组需求量的代表值，计算出各组的频率为概率，频率最大对应的需求量即为需求量的众数，各组代表需求量与对应的频率的和就是需求量的平均数；（2）由已知条件推导出当100≤x≤160时，y=50x-（160-x）30=80x-1800，当160＜x≤200时，y=160×50=8000，由此能将Y表示为X的函数，（3）根据（2）中利润与需求量的关系式，令y大于等于4800，列出关于需求量的不等式，求出需求量x的取值范围，再根据题中的频率分布表计算出对应的概率.
试题解析：（1）由频率直方图得到：
需求量为110的频率=0.005×20=0.1，
需求量为130的频率=0.01×20=0.2，
需求量为150的频率=0.015×20=0.3，
需求量为170的频率=0.0125×20=0.25，
需求量为190的频率=0.0075×20=0.15，
∴这个开学季内市场需求量X的众数是150，
这个开学季内市场需求量X的平均数：
=110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153． 4分
（2）∵每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元，
∴当100≤x≤160时，
y=50x-（160-x）30=80x-1800，
当160＜x≤200时，
y=160×50=8000，
∴y=8分
（3）∵利润不少于4800元，
∴80x-4800≥4800，解得x≥120，
∴由（1）知利润不少于4800元的概率p=1-0.1=0.9． 12分
考点:离散型随机变量的期望与方差，频率分布直方图应用，众数、中位数、平均数，分段函数函数解析式，概率的估计
