题目内容
已知函数 ,其中
,其中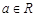 .
.
(1)若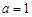 ,求函数
,求函数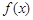 的极值点;
的极值点;
(2)若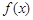 在区间
在区间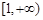 内单调递增,求实数
内单调递增,求实数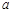 的取值范围.
的取值范围.
(1)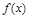 有极小值点
有极小值点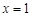 ,无极大值点;(2)[1,+∞)。
,无极大值点;(2)[1,+∞)。
解析试题分析:(1)先求出函数的定义域,求出函数的导数,求出导数为0的点,确定导数为0和导数不存在点的点的左右两侧导函数的符号,确定函数的单调性,若单调性相同不是极值点,若左增右减是极大值点,若左减右增是极小值点;(2)先求出导数,利用导数与函数单调性关系,将函数在[1,+∞)上是增函数问题转化为导函数大于等于0在[1,+∞)上恒成立问题,通过参变分离,转化为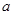 ≥
≥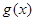 在[1,+∞)恒成立问题,求出
在[1,+∞)恒成立问题,求出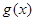 在[1,+∞)的最大值
在[1,+∞)的最大值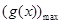 ,则
,则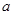 ≥
≥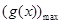 .
.
试题解析:(1)当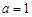 时,
时,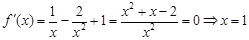 或
或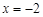 ……3分
……3分
所以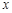
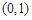
1 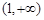
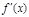
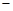
0 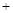
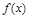
单调减 极小值 单调增 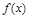 有极小值点
有极小值点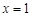 ,无极大值点……6分
,无极大值点……6分
(2)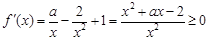 ,所以
,所以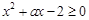
 对
对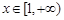 恒成立……9分
恒成立……9分
又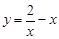 在
在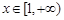 上单调递减,所以
上单调递减,所以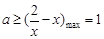 .……12分
.……12分
考点:1.利用导数求函数极值;2.函数单调性与导数关系;3.转化与化归思想.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
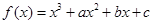 在
在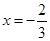 与
与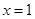 时都取得极值
时都取得极值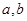 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式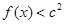 恒成立,求
恒成立,求 的取值范围
的取值范围  .
. 的图象在
的图象在 处的切线方程;
处的切线方程; 对任意的
对任意的 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. .
. 且
且 时,证明:
时,证明: ;
; ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,证明:
时,证明: .
. ,其中
,其中 .
.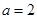 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;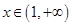 ,都有
,都有 ,求
,求 的取值范围.
的取值范围. 的图像与直线
的图像与直线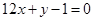 相切于点
相切于点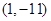 .
.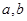 的值;
的值; 的单调性.
的单调性.
 时,求
时,求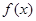 的极值;
的极值; 时,讨论
时,讨论 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.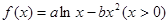 ,若函数
,若函数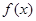 在
在 处与直线
处与直线 相切,
相切,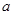 ,
, 的值;(2)求函数
的值;(2)求函数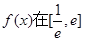 上的最大值.
上的最大值.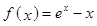 (e为自然对数的底数)
(e为自然对数的底数)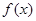 的最小值;
的最小值;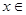
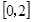 ,不等式
,不等式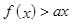 恒成立,求实数
恒成立,求实数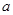 的取值范围.
的取值范围.