题目内容
定义在实数集上的函数 .
.
⑴求函数 的图象在
的图象在 处的切线方程;
处的切线方程;
⑵若 对任意的
对任意的 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
⑴ ;⑵实数m的取值范围
;⑵实数m的取值范围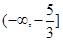 .
.
解析试题分析:⑴曲线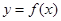 在点
在点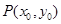 处的切线方程为:
处的切线方程为: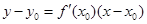 ,所以求出导数及切点即得切线方程;⑵
,所以求出导数及切点即得切线方程;⑵ 可化为
可化为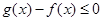 ,令
,令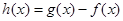 ,则只需
,则只需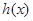 的最小值小于等于0即可.下面就利用导数求
的最小值小于等于0即可.下面就利用导数求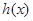 的最小值然后解不等式即可得实数m的取值范围.
的最小值然后解不等式即可得实数m的取值范围.
试题解析:⑴∵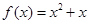 ,当
,当 时,
时,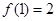
∵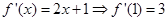
∴所求切线方程为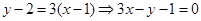 . .(4分)
. .(4分)
⑵令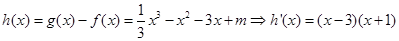
∴当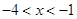 时,
时,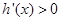 ;
;
当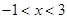 时,
时,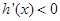 ;
;
当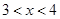 时,
时,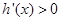 ;
;
要使 恒成立,即
恒成立,即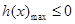 .
.
由上知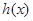 的最大值在
的最大值在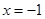 或
或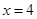 取得.
取得.
而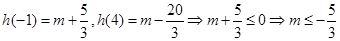
∴实数m的取值范围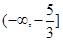 . 13分
. 13分
考点:1、导数的应用;2、导数与不等式.

练习册系列答案
相关题目
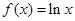 ,
,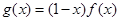
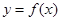 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;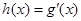 及
及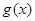 在区间
在区间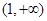 上的单调性;
上的单调性;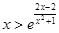 在
在 函数
函数 在
在 上是单调递减函数,
上是单调递减函数, 方程
方程 无实根,若“
无实根,若“ 或
或 ”为真,“
”为真,“ 的取值范围。
的取值范围。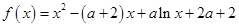 (其中
(其中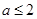 ).
).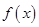 的单调区间;
的单调区间;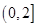 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围.
的取值范围. 为函数
为函数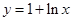 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线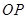 的斜率
的斜率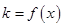 .
.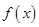 在区间
在区间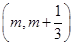
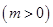 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;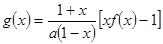 ,若对任意
,若对任意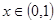 恒有
恒有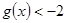 ,求实数
,求实数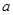 的取值范围.
的取值范围. ,(
,( ).
). 有最值,求实数
有最值,求实数 的取值范围;
的取值范围; 时,若存在
时,若存在 、
、
 ,使得曲线
,使得曲线 在
在 与
与 处的切线互相平行,求证:
处的切线互相平行,求证: .
. ,其中
,其中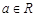 .
.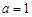 ,求函数
,求函数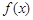 的极值点;
的极值点;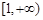 内单调递增,求实数
内单调递增,求实数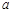 的取值范围.
的取值范围.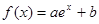 在
在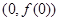 处切线为
处切线为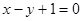 .
.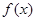 的解析式;
的解析式;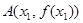 ,
,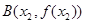 ,
,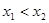 ,
,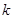 表示直线
表示直线 的斜率,求证:
的斜率,求证: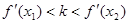 .
.