题目内容
设函数 的图像与直线
的图像与直线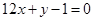 相切于点
相切于点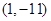 .
.
(1)求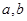 的值;
的值;
(2)讨论函数 的单调性.
的单调性.
(1)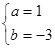 (2)单调递减区间为
(2)单调递减区间为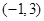 ,单调递增区间为
,单调递增区间为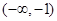 ,
,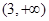 .
.
解析试题分析:(1)先求出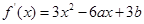 ,结合题中所给的切线与切点可得方程组
,结合题中所给的切线与切点可得方程组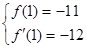 ,从而求解方程组即可得到
,从而求解方程组即可得到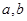 的值;(2)由(1)中所求得的
的值;(2)由(1)中所求得的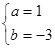 ,确定
,确定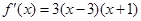 ,从而由
,从而由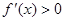 ,可求出函数
,可求出函数 的单调增区间,由
的单调增区间,由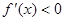 ,可求出函数
,可求出函数 的单调减区间.
的单调减区间.
试题解析:(1) 求导得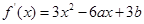 ,又因为
,又因为 的图像与直线
的图像与直线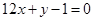 相切于点
相切于点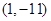
所以有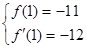 即
即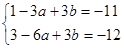 解得
解得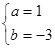
(2)由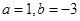 得
得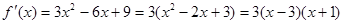
当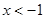 或
或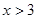 时,
时,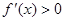 ,
,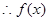 的单调递增区间为
的单调递增区间为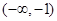 ,
,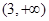
当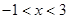 时,
时,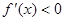 ,
,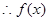 的单调递减区间为
的单调递减区间为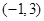 .
.
考点:1.导数的几何意义;2.函数的单调性与导数.

练习册系列答案
相关题目
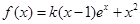 .
. ,求函数
,求函数 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;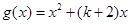 的图象恒在
的图象恒在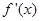 图象的上方,求k的取值范围;
图象的上方,求k的取值范围; 为函数
为函数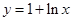 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线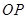 的斜率
的斜率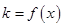 .
.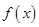 在区间
在区间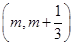
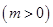 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;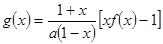 ,若对任意
,若对任意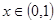 恒有
恒有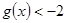 ,求实数
,求实数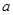 的取值范围.
的取值范围. .
. 的单调区间;
的单调区间; 时,求证:
时,求证: 恒成立..
恒成立.. ,其中
,其中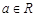 .
.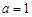 ,求函数
,求函数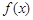 的极值点;
的极值点;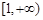 内单调递增,求实数
内单调递增,求实数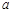 的取值范围.
的取值范围. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;  求函数
求函数 的单调区间.
的单调区间. -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0). 与直线
与直线 ,
, ,
, 所围成平面图形的面积.
所围成平面图形的面积.
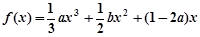 ,
,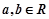 ,
,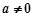 ,
, 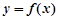 与
与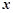 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为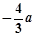 ,求
,求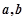 的值;
的值;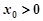 ,且
,且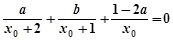 ,
,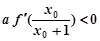 ; ②求证:
; ②求证: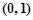 上存在极值点.
上存在极值点.