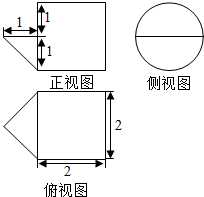
题目内容
1.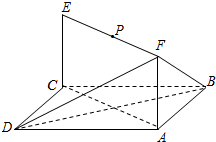 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2},AF=1$.P为线段EF上一点.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2},AF=1$.P为线段EF上一点.(I)若P为EF的中点,求证:AP⊥DF;
(Ⅱ)是否存在点P,使直线AP与平面BDF所成的角为$\frac{π}{3}$?若存在,确定P点的位置;若不存在,说明理由.
分析 (I)建立空间坐标系,由条件求得点P的坐标,再根据向量$\overrightarrow{AP}$与向量$\overrightarrow{DP}$的数量级等于零,可得AP⊥DF.
(II)设平面BDF的法向量为$\overrightarrow n=(x,y,z)$,由 $\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{DB}=0}\\{\overrightarrow n•\overrightarrow{DF}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=y}\\{z=-\sqrt{2}y}\end{array}}\right.$,取$\overrightarrow n=(1,1,-\sqrt{2})$,设$\overrightarrow{EP}=λ\overrightarrow{EF}⇒P(\sqrt{2}λ,\sqrt{2}λ,1)$,再根据$\overrightarrow{AP}$与$\overrightarrow{n}$的夹角的余弦值的绝对值为$\frac{\sqrt{3}}{2}$,求得λ的值,可得结论.
解答 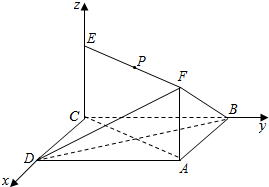 解:(I)以CD,CB,CE分别为x,y,z轴建立空间直角坐标系如图.
解:(I)以CD,CB,CE分别为x,y,z轴建立空间直角坐标系如图.
则$C(0,0,0),A(\sqrt{2},\sqrt{2},0),B(0,\sqrt{2},0),D(\sqrt{2},0,0),F(\sqrt{2},\sqrt{2},1)$.
∵P为EF的中点,∴$P(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2},1)$$⇒\overrightarrow{AP}=(-\frac{{\sqrt{2}}}{2},-\frac{{\sqrt{2}}}{2},1),\overrightarrow{DF}=(0,\sqrt{2},0)$,$⇒\overrightarrow{AP}•\overrightarrow{DF}=-\frac{{\sqrt{2}}}{2}×\sqrt{2}+1=0∴AP⊥DF$.
(II)由(I)得,$\overrightarrow{DB}=(-\sqrt{2},\sqrt{2},0),\overrightarrow{DF}=(0,\sqrt{2},1)$.
设平面BDF的法向量为$\overrightarrow n=(x,y,z)$,由 $\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{DB}=0}\\{\overrightarrow n•\overrightarrow{DF}=0}\end{array}}\right.⇒\left\{{\begin{array}{l}{x=y}\\{z=-\sqrt{2}y}\end{array}}\right.$,
取$\overrightarrow n=(1,1,-\sqrt{2})$,设$\overrightarrow{EP}=λ\overrightarrow{EF}⇒P(\sqrt{2}λ,\sqrt{2}λ,1)$,
则$\overrightarrow{AP}=(\sqrt{2}λ-\sqrt{2},\sqrt{2}λ-\sqrt{2},1)(0≤λ≤1)$,$\overrightarrow n•\overrightarrow{AP}=2\sqrt{2}λ-3\sqrt{2}$,
而$|\overrightarrow n|=2,|\overrightarrow{AP}|=\sqrt{4{{(λ-1)}^2}+1}$,∴$\frac{{|2\sqrt{2}λ-3\sqrt{2}|}}{{2\sqrt{{{(λ-1)}^2}+1}}}=\frac{{\sqrt{3}}}{2}⇒4{λ^2}=3∴λ=\frac{{\sqrt{3}}}{2}∈[0,1]$,
即$EP=\sqrt{3}$所以存在P点($EP=\sqrt{3}$),使直线AP与平面BDF成60°.
点评 本题主要考查直线和平面所成的角,空间向量的应用,体现了转化的数学思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{8}{3}$ | B. | $\frac{4}{5}$ | C. | 4 | D. | $\frac{1}{4}$ |
 小明同学只做了一个简易的网球发射器,可用于帮忙联系定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球同底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系xOy,x轴在地平面上的球场中轴线上,y轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程y=$\frac{1}{2}$kx-$\frac{1}{80}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.发射器的射程是指网球落地点的横坐标.
小明同学只做了一个简易的网球发射器,可用于帮忙联系定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球同底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系xOy,x轴在地平面上的球场中轴线上,y轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程y=$\frac{1}{2}$kx-$\frac{1}{80}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.发射器的射程是指网球落地点的横坐标.