题目内容
4．
如图，一栋建筑物AB的高为（30-10$\sqrt{3}$）m，在该建筑物的正东方向有一个通信塔CD，在它们之间的地面点M（B，M，D三点共线）处测得楼顶A，塔顶C的仰角分别是15°和60°，在楼顶A处测得塔顶C的仰角为30°，则通信塔CD的高为（ ）| A． | 30m | B． | 60m | C． | 30$\sqrt{3}$m | D． | 40$\sqrt{3}$m |
分析 设AE⊥CD，垂足为E，在△AMC中，利用正弦定理，求出AC，即可得出结论．
解答 解：设AE⊥CD，垂足为E，则
在△AMC中，AM=$\frac{AB}{sin15°}$=20$\sqrt{6}$，∠AMC=105°，∠C=30°，
∴$\frac{AC}{sin105°}=\frac{20\sqrt{6}}{sin30°}$，
∴AC=60+20$\sqrt{3}$，
∴$CE=30+10\sqrt{3}$，
∴CD=30-10$\sqrt{3}$+30+10$\sqrt{3}$=60，
故选：B．
点评 本题考查利用数学知识解决实际问题，考查正弦定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目
15．观察下列的图形中小正方形的个数，则第6个图中有（ ）个小正方形，第n个图中有（ ）个小正方形（ ）
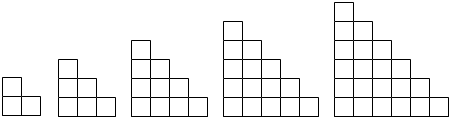
| A． | 28，$\frac{（n+1）（n+2）}{2}$ | B． | 14，$\frac{（n+1）（n+2）}{2}$ | C． | 28，$\frac{n}{2}$ | D． | 12，$\frac{{n}^{2}+n}{2}$ |
19．函数y=${log_{\frac{1}{2}}}$（3x-x2-2）的单调递减区间是（ ）
| A． | （1，2） | B． | （2，+∞） | C． | （1，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，+∞） |
9．已知点P在曲线C：y2=4-2x2上，点A（0，-$\sqrt{2}$），则|PA|的最大值为（ ）
| A． | 2-$\sqrt{2}$ | B． | 2+$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{2}$+1 |
16．已知向量$\overrightarrow{a}$=（2，4），$\overrightarrow{b}$=（-1，1），则2$\overrightarrow{a}$+$\overrightarrow{b}$等于（ ）
| A． | （5，7） | B． | （5，9） | C． | （3，7） | D． | （3，9） |