题目内容
【题目】已知函数![]() ,
, 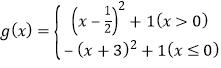 则方程g[f(x)]﹣a=0(a为正实数)的实数根最多有( )个.
则方程g[f(x)]﹣a=0(a为正实数)的实数根最多有( )个.
A.6个
B.4个
C.7个
D.8个
【答案】A
【解析】解:∵函数![]() ,
, 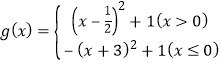 ,
,
令f′(x)=0 可得 x=0,x=2,在(﹣∞,0)上,f′(x)>0,f(x)是增函数;
在(0,2)上,f′(x)<0,f(x)是减函数;在(2,+∞)上,f′(x)>0,f(x)是增函数.
故f(x)的极大值为f(0)=1,极小值为f(2)=﹣3,且函数的值域为R.
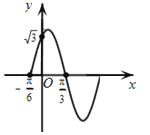
由函数g(x)的图象可得,当x=﹣3或x=![]() 时,g(x)=1.
时,g(x)=1.
①当a=1时,若方程g[f(x)]﹣a=0,则:
f(x)=﹣3,此时方程有2个根,或f(x)=![]() , 此时方程有3个根,
, 此时方程有3个根,
故方程g[f(x)]﹣a=0可能共有5个根.
②当0<a<1时,方程g[f(x)]﹣a=0,则:
f(x)∈(﹣4,﹣3),此时方程有1个根,或f(x)∈(﹣3,﹣2),此时方程有3个根
故方程g[f(x)]﹣a=0可能共有4个根.
③当a>1时,方程g[f(x)]﹣a=0,则:f(x)∈(0,![]() ),或f(x)∈(
),或f(x)∈(![]() , +∞),
, +∞),
方程可能有4个、5个或6个根.
故方程g[f(x)]﹣a=0(a为正实数)的实数根最多有6个,
故选 A.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目