题目内容
已知函数y=f(x)是周期为2的周期函数,且当x∈[-1,1]时,f(x)=2|x|-1,则函数F(x)=f(x)-|lgx|的零点个数是( )
| A、9 | B、10 | C、11 | D、12 |
考点:根的存在性及根的个数判断,函数的周期性
专题:函数的性质及应用
分析:在坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,分析两个图象交点的个数,进而可得函数F(x)=f(x)-|lgx|的零点个数.
解答:解:∵函数F(x)=f(x)-|lgx|的零点,
即为函数y1=|lgx|,y2=f(x)的图象的交点,
又∵函数y=f(x)是周期为2的周期函数,
且当x∈[-1,1]时,f(x)=2|x|-1,
在同一坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,如下图所示:
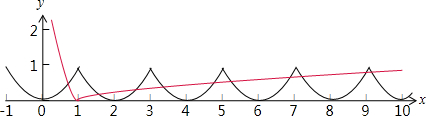
由图可知:两个函数y1=|lgx|,y2=f(x)的图象共有10个交点,
故函数F(x)=f(x)-|lgx|有10个零点,
故选:B.
即为函数y1=|lgx|,y2=f(x)的图象的交点,
又∵函数y=f(x)是周期为2的周期函数,
且当x∈[-1,1]时,f(x)=2|x|-1,
在同一坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,如下图所示:

由图可知:两个函数y1=|lgx|,y2=f(x)的图象共有10个交点,
故函数F(x)=f(x)-|lgx|有10个零点,
故选:B.
点评:本题考查了函数零点、对应方程的根和函数图象之间的关系,通过转化和作图求出函数零点的个数.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||
|
| A、(0,2) |
| B、(0,2] |
| C、(2,+∞) |
| D、[2,+∞) |
若函数y=f(x)是定义域在R上的奇函数,且在(0,+∞)上是增函数,f(2)=3,则不等式f(x)+3≤0的解集为( )
| A、[2,+∞) | B、[-2,2] | C、(-∞,-2] | D、(-∞,-2]∪[2,+∞) |
函数y=f(x)的图象与函数y=g(x)的图象关于直线x+y=0对称,则y=f(x)的反函数是( )
| A、y=g(x) | B、y=g(-x) | C、y=-g(x) | D、y=-g(-x) |
函数f(x)=2x-
的零点所在的区间可能是( )
| 1 |
| x |
| A、(1,+∞) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
方程x3-x-1=0的实数解落在区间( )
| A、(-1,0) | B、(0,1) | C、(2,3) | D、(1,2) |
设f(x)=
,若对任意x1,x2,都有
<0,则实数a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,0] |
| B、[0,+∞) |
| C、[-1,0] |
| D、[0,1] |
在数列{an}中,设S0=0,Sn=a1+a2+a3+…+an,其中ak=
,1≤k≤n,k,n∈N*,当n≤14时,使Sn=0的n的最大值为 ( )
|
| A、11 | B、12 | C、13 | D、14 |
已知圆锥的正视图和侧视图都是边长为4的等边三角形,则此圆锥的表面积是( )
| A、4π | ||
| B、8π | ||
C、
| ||
| D、12π |