题目内容
若存在实常数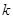 和
和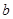 ,使得函数
,使得函数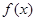 和
和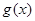 对其定义域上的任意实数
对其定义域上的任意实数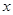 分别满足:
分别满足: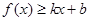 和
和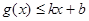 ,则称直线
,则称直线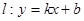 为
为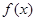 和
和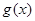 的“隔离直线”.已知
的“隔离直线”.已知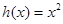 ,
,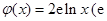 为自然对数的底数).
为自然对数的底数).
(1)求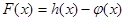 的极值;
的极值;
(2)函数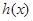 和
和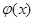 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
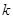 和
和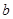 ,使得函数
,使得函数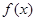 和
和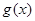 对其定义域上的任意实数
对其定义域上的任意实数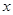 分别满足:
分别满足: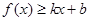 和
和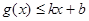 ,则称直线
,则称直线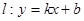 为
为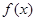 和
和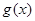 的“隔离直线”.已知
的“隔离直线”.已知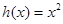 ,
,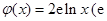 为自然对数的底数).
为自然对数的底数).(1)求
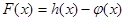 的极值;
的极值;(2)函数
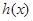 和
和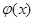 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.(1)当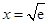 时,
时,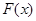 取极小值,其极小值为
取极小值,其极小值为 (2)函数
(2)函数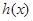 和
和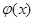 存在唯一的隔离直线
存在唯一的隔离直线
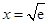 时,
时,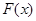 取极小值,其极小值为
取极小值,其极小值为 (2)函数
(2)函数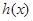 和
和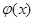 存在唯一的隔离直线
存在唯一的隔离直线
试题分析:(1)
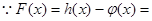
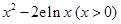 ,
, 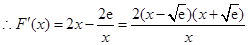 .
. 当
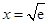 时,
时,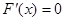 .
. 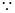 当
当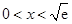 时,
时,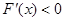 ,此时函数
,此时函数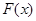 递减;
递减; 当
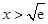 时,
时,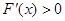 ,此时函数
,此时函数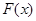 递增;
递增;∴当
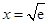 时,
时,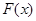 取极小值,其极小值为
取极小值,其极小值为 . …………………………………6分
. …………………………………6分 (2)解法一:由(1)可知函数
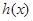 和
和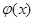 的图象在
的图象在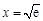 处有公共点,因此若存在
处有公共点,因此若存在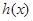 和
和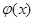 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点. 设隔离直线的斜率为
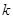 ,则直线方程为
,则直线方程为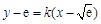 ,即
,即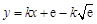 .
. 由
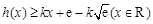 ,可得
,可得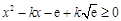 当
当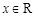 时恒成立.
时恒成立. ,
, 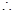 由
由 ,得
,得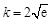 .
. 下面证明
 当
当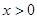 时恒成立.
时恒成立.令
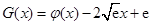
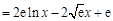 ,则
,则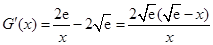 ,
, 当
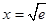 时,
时,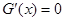 .
.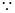 当
当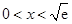 时,
时,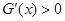 ,此时函数
,此时函数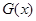 递增;
递增;当
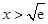 时,
时,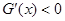 ,此时函数
,此时函数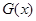 递减;
递减;∴当
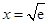 时,
时,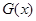 取极大值,其极大值为
取极大值,其极大值为 .
. 从而
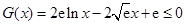 ,即
,即 恒成立.
恒成立. ∴函数
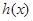 和
和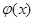 存在唯一的隔离直线
存在唯一的隔离直线 .……………12分
.……………12分 解法二: 由(1)可知当
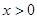 时,
时,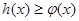 (当且仅当
(当且仅当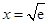 时取等号) .
时取等号) . 若存在
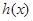 和
和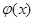 的隔离直线,则存在实常数
的隔离直线,则存在实常数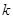 和
和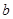 ,使得
,使得 和
和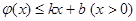 恒成立,
恒成立,令
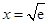 ,则
,则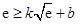 且
且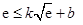
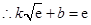 ,即
,即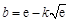 .
. 后面解题步骤同解法一.
点评:求函数极值要首先确定定义域,通过导数等于零找到极值点,但要说明是极大值还是极小值,第二问中将不等式恒成立问题转化为求函数最值问题,这种转化思路是函数综合题中常用的思路,其中找到函数
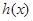 和
和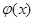 的图象在
的图象在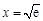 处有公共点是求解的关键
处有公共点是求解的关键
练习册系列答案
相关题目
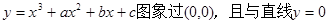 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为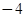 ;
;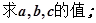

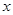 的不等式
的不等式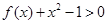
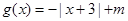 ,
,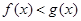 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围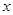 次之间的关系为Z=
次之间的关系为Z=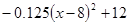 ,1≤
,1≤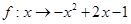 是集合
是集合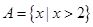 到集合
到集合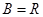 的映射。若对于实数
的映射。若对于实数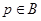 ,在
,在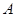 中不存在对应的元素,则实数
中不存在对应的元素,则实数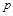 的取值范围是( )
的取值范围是( )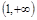 B.
B. 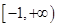 C.
C. 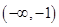 D.
D. 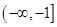
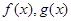 是定义在R上可导函数,满足
是定义在R上可导函数,满足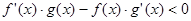 ,且
,且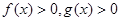 ,对
,对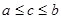 时。下列式子正确的是( )
时。下列式子正确的是( )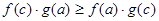
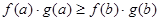
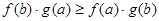

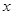 元/千克,政府补贴为
元/千克,政府补贴为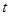 元/千克,根据市场调查,当
元/千克,根据市场调查,当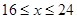 时,这种食品市场日供应量
时,这种食品市场日供应量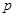 万千克与市场日需量
万千克与市场日需量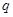 万千克近似地满足关系:
万千克近似地满足关系: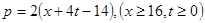 ,
,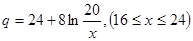 。当
。当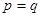 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。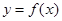 在区间(
在区间(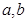 )的导函数
)的导函数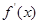 ,
,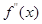 ,若在区间(
,若在区间(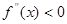 恒成立,则称函数
恒成立,则称函数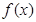 在区间(
在区间(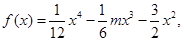 若当实数
若当实数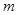 满足
满足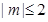 时,函数
时,函数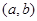 上为凸函数,则
上为凸函数,则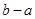 最大值 ( )
最大值 ( )