题目内容
设函数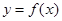 在区间(
在区间(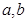 )的导函数
)的导函数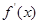 ,
,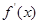 在区间(
在区间(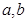 )的导函数
)的导函数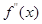 ,若在区间(
,若在区间(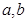 )上
)上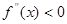 恒成立,则称函数
恒成立,则称函数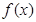 在区间(
在区间(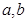 )为凸函数,已知
)为凸函数,已知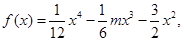 若当实数
若当实数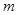 满足
满足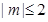 时,函数
时,函数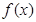 在
在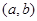 上为凸函数,则
上为凸函数,则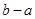 最大值 ( )
最大值 ( )
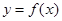 在区间(
在区间(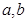 )的导函数
)的导函数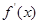 ,
,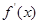 在区间(
在区间(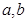 )的导函数
)的导函数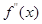 ,若在区间(
,若在区间(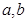 )上
)上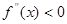 恒成立,则称函数
恒成立,则称函数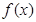 在区间(
在区间(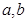 )为凸函数,已知
)为凸函数,已知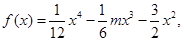 若当实数
若当实数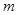 满足
满足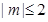 时,函数
时,函数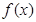 在
在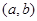 上为凸函数,则
上为凸函数,则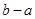 最大值 ( )
最大值 ( )| A.1 | B.2 | C.3 | D.4 |
D
试题分析:
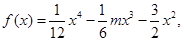
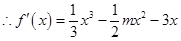 ,
,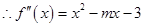 ,函数
,函数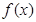 在
在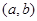 上为凸函数,
上为凸函数,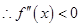 对于
对于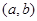 恒成立,
恒成立,设函数
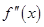 与x轴交点横坐标为
与x轴交点横坐标为 ,
,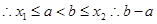 的最大值为
的最大值为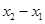
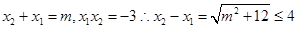
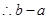 最大值为4
最大值为4点评:本题根据题目中凸函数的定义可知对于函数
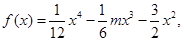 满足性质
满足性质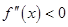 对于
对于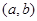 恒成立,进而结合二次函数性质求得
恒成立,进而结合二次函数性质求得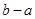 最大值
最大值
练习册系列答案
相关题目
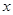 表示P点行程,
表示P点行程,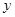 表PA的长,求
表PA的长,求
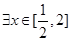 ,使
,使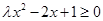 成立,则实数
成立,则实数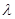 的取值范围为( )
的取值范围为( )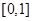
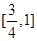
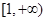
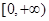
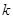 和
和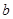 ,使得函数
,使得函数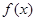 和
和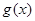 对其定义域上的任意实数
对其定义域上的任意实数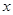 分别满足:
分别满足: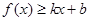 和
和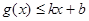 ,则称直线
,则称直线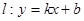 为
为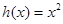 ,
,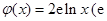 为自然对数的底数).
为自然对数的底数).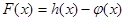 的极值;
的极值;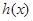 和
和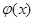 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
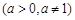 .若数列
.若数列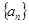 满足
满足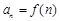 且
且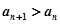
 ,则实数
,则实数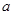 的取值范围是
的取值范围是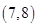
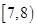
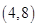
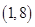
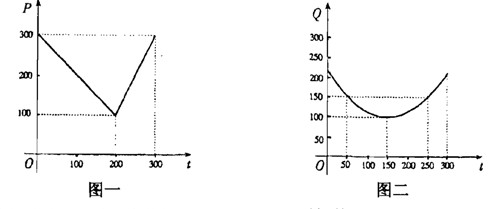
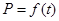 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式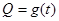 .
.
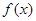 为定义在
为定义在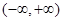 上的可导函数,且
上的可导函数,且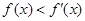 对于
对于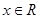 恒成立,且
恒成立,且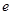 为自然对数的底,则( )
为自然对数的底,则( )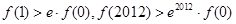
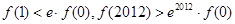
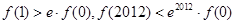
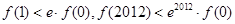
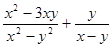 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;